为什么 HashTable 慢? 它的并发度是什么? 那么 ConcurrentHashMap 并发度是什么?
ConcurrentHashMap 在 Java7 和 Java8 中实现有什么差别?Java8 解決了 Java7 中什么问题?
ConcurrentHashMap JDK1.7 实现的原理是什么?
ConcurrentHashMap JDK1.8 实现的原理是什么?
ConcurrentHashMap JDK1.7 中 Segment 数 (concurrencyLevel) 默认值是多少?为何一旦初始化就不可再扩容?
ConcurrentHashMap JDK1.7 说说其 put 的机制?
ConcurrentHashMap JDK1.7 是如何扩容的?
ConcurrentHashMap JDK1.8 是如何扩容的?
ConcurrentHashMap JDK1.8 链表转红黑树的时机是什么? 临界值为什么是 8?
ConcurrentHashMap JDK1.8 是如何进行数据迁移的?
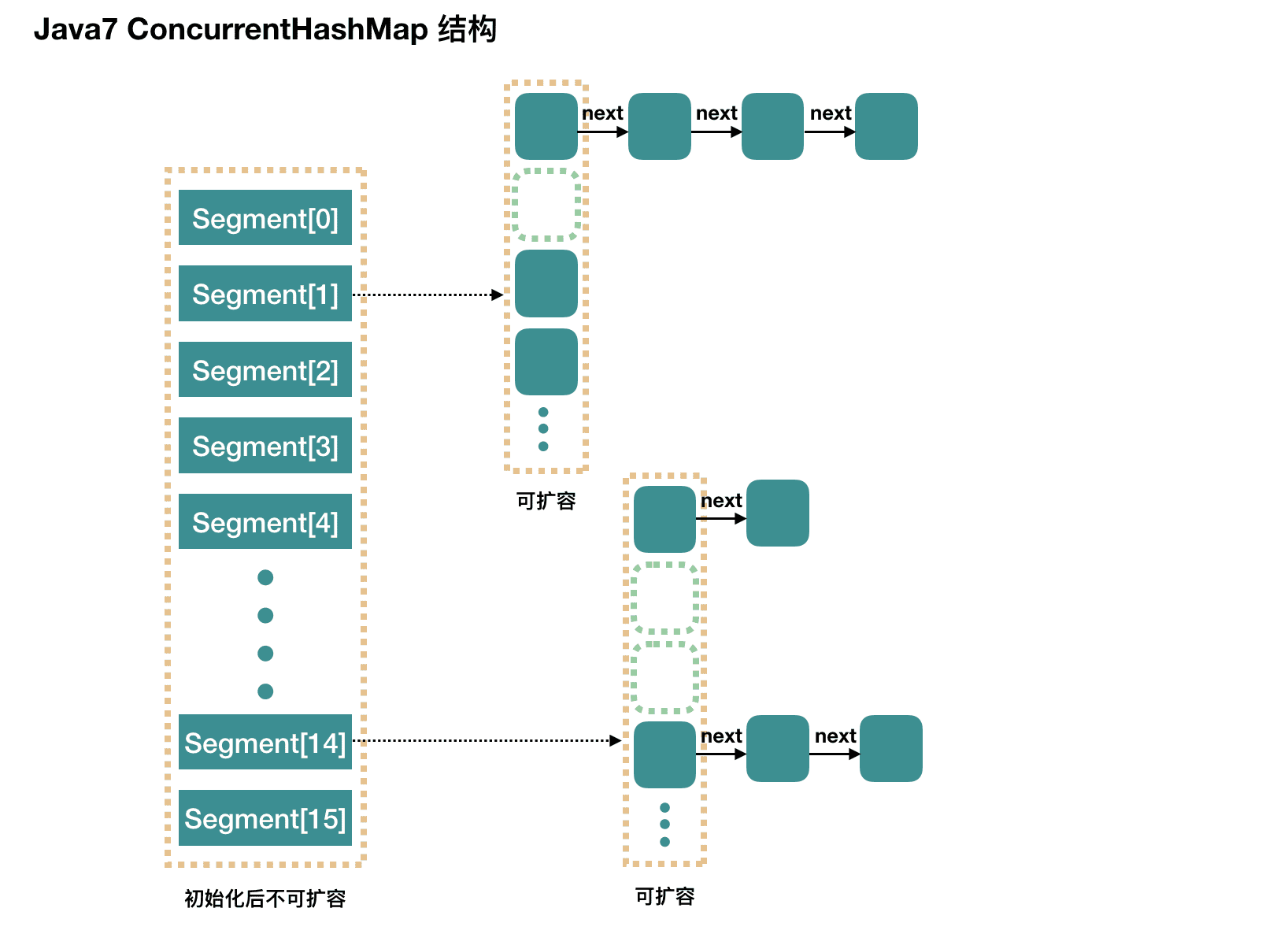
JDK 1.7 在 JDK 1.5 ~ 1.7 版本中,Java 使用 分段锁机制 实现 ConcurrentHashMap
ConcurrentHashMap 在对象中保存了一个 Segment 数组,即将整个 Hash 表划分为多个分段。而每个 Segment 元素,即每个分段则类似于一个 Hashtable。这样,在执行 put 操作时首先根据 hash 算法定位到元素属于哪个 Segment,然后对该 Segment 加锁即可。因此,ConcurrentHashMap 在多线程并发编程中可是实现线程安全的 put 操作
数据结构 关键属性:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 static final int DEFAULT_INITIAL_CAPACITY = 16 ;static final float DEFAULT_LOAD_FACTOR = 0.75f ;static final int DEFAULT_CONCURRENCY_LEVEL = 16 ;static final int MAXIMUM_CAPACITY = 1 << 30 ;static final int MIN_SEGMENT_TABLE_CAPACITY = 2 ;static final int MAX_SEGMENTS = 1 << 16 ; static final int RETRIES_BEFORE_LOCK = 2 ;final Segment<K,V>[] segments;
关键内部类:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 static final class Segment <K,V> extends ReentrantLock implements Serializable { static final int MAX_SCAN_RETRIES = Runtime.getRuntime().availableProcessors() > 1 ? 64 : 1 ; transient volatile HashEntry<K,V>[] table; transient int count; transient int modCount; transient int threshold; final float loadFactor; Segment(float lf, int threshold, HashEntry<K,V>[] tab) { this .loadFactor = lf; this .threshold = threshold; this .table = tab; } }
HashEntry
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 static final class HashEntry <K,V> { final int hash; final K key; volatile V value; volatile HashEntry<K,V> next; HashEntry(int hash, K key, V value, HashEntry<K,V> next) { this .hash = hash; this .key = key; this .value = value; this .next = next; } final void setNext (HashEntry<K,V> n) { UNSAFE.putOrderedObject(this , nextOffset, n); } static final sun.misc.Unsafe UNSAFE; static final long nextOffset; static { try { UNSAFE = sun.misc.Unsafe.getUnsafe(); Class k = HashEntry.class; nextOffset = UNSAFE.objectFieldOffset (k.getDeclaredField("next" )); } catch (Exception e) { throw new Error (e); } } }
ConcurrentHashMap 是一个 Segment 数组,Segment 通过继承 ReentrantLock 来进行加锁 ,所以每次需要加锁的操作锁住的是一个 segment,这样只要保证每个 Segment 是线程安全的,也就实现了全局的线程安全
初始化 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public ConcurrentHashMap (int initialCapacity, float loadFactor, int concurrencyLevel) { if (!(loadFactor > 0 ) || initialCapacity < 0 || concurrencyLevel <= 0 ) throw new IllegalArgumentException (); if (concurrencyLevel > MAX_SEGMENTS) concurrencyLevel = MAX_SEGMENTS; int sshift = 0 ; int ssize = 1 ; while (ssize < concurrencyLevel) { ++sshift; ssize <<= 1 ; } this .segmentShift = 32 - sshift; this .segmentMask = ssize - 1 ; if (initialCapacity > MAXIMUM_CAPACITY) initialCapacity = MAXIMUM_CAPACITY; int c = initialCapacity / ssize; if (c * ssize < initialCapacity) ++c; int cap = MIN_SEGMENT_TABLE_CAPACITY; while (cap < c) cap <<= 1 ; Segment<K,V> s0 = new Segment <K,V>(loadFactor, (int )(cap * loadFactor), (HashEntry<K,V>[])new HashEntry [cap]); Segment<K,V>[] ss = (Segment<K,V>[])new Segment [ssize]; UNSAFE.putOrderedObject(ss, SBASE, s0); this .segments = ss; }
初始化过程主要是为了计算出 Segment 数组的大小
其中需要注意的是,初始化只会创建一个 Segment s0 放入 Segment 数组中
Segment 默认的容量为 2,负载因子 0.75,这样插入第一个元素不会扩容,插入第二个才会进行扩容
segmentShift 和 segmentMask 这两个属性仅赋值,还未知其作用
PUT 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public V put (K key, V value) { Segment<K,V> s; if (value == null ) throw new NullPointerException (); int hash = hash(key); int j = (hash >>> segmentShift) & segmentMask; if ((s = (Segment<K,V>)UNSAFE.getObject (segments, (j << SSHIFT) + SBASE)) == null ) s = ensureSegment(j); return s.put(key, hash, value, false ); }
s = (Segment<K,V>) UNSAFE.getObject(segments, (j << SSHIFT) + SBASE) 这里是直接通过计算 segment 数组中元素的内存偏移量来获取元素
具体看下初始化指定位置的 segment
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 private Segment<K,V> ensureSegment (int k) { final Segment<K,V>[] ss = this .segments; long u = (k << SSHIFT) + SBASE; Segment<K,V> seg; if ((seg = (Segment<K,V>)UNSAFE.getObjectVolatile(ss, u)) == null ) { Segment<K,V> proto = ss[0 ]; int cap = proto.table.length; float lf = proto.loadFactor; int threshold = (int )(cap * lf); HashEntry<K,V>[] tab = (HashEntry<K,V>[])new HashEntry [cap]; if ((seg = (Segment<K,V>)UNSAFE.getObjectVolatile(ss, u)) == null ) { Segment<K,V> s = new Segment <K,V>(lf, threshold, tab); while ((seg = (Segment<K,V>)UNSAFE.getObjectVolatile(ss, u)) == null ) { if (UNSAFE.compareAndSwapObject(ss, u, null , seg = s)) break ; } } } return seg; }
接下来就到了 Segment 的内部方法中
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 final V put (K key, int hash, V value, boolean onlyIfAbsent) { HashEntry<K,V> node = tryLock() ? null : scanAndLockForPut(key, hash, value); V oldValue; try { HashEntry<K,V>[] tab = table; int index = (tab.length - 1 ) & hash; HashEntry<K,V> first = entryAt(tab, index); for (HashEntry<K,V> e = first;;) { if (e != null ) { K k; if ((k = e.key) == key || (e.hash == hash && key.equals(k))) { oldValue = e.value; if (!onlyIfAbsent) { e.value = value; ++modCount; } break ; } e = e.next; } else { if (node != null ) node.setNext(first); else node = new HashEntry <K,V>(hash, key, value, first); int c = count + 1 ; if (c > threshold && tab.length < MAXIMUM_CAPACITY) rehash(node); else setEntryAt(tab, index, node); ++modCount; count = c; oldValue = null ; break ; } } } finally { unlock(); } return oldValue; }
put 过程中涉及两个关键方法:scanAndLockForPut 和 rehash
scanAndLockForPut 是在 tryLock 尝试获取独占锁失败后执行的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 private HashEntry<K,V> scanAndLockForPut (K key, int hash, V value) { HashEntry<K,V> first = entryForHash(this , hash); HashEntry<K,V> e = first; HashEntry<K,V> node = null ; int retries = -1 ; while (!tryLock()) { HashEntry<K,V> f; if (retries < 0 ) { if (e == null ) { if (node == null ) node = new HashEntry <K,V>(hash, key, value, null ); retries = 0 ; } else if (key.equals(e.key)) retries = 0 ; else e = e.next; } else if (++retries > MAX_SCAN_RETRIES) { lock(); break ; } else if ((retries & 1 ) == 0 && (f = entryForHash(this , hash)) != first) { e = first = f; retries = -1 ; } } return node; }
简单理解下来就如方法名的意思一样,为 put 遍历相关节点以及关键的获取独占锁
另一个关键方法就是 rehash 扩容方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 private void rehash (HashEntry<K,V> node) { HashEntry<K,V>[] oldTable = table; int oldCapacity = oldTable.length; int newCapacity = oldCapacity << 1 ; threshold = (int )(newCapacity * loadFactor); HashEntry<K,V>[] newTable = (HashEntry<K,V>[]) new HashEntry [newCapacity]; int sizeMask = newCapacity - 1 ; for (int i = 0 ; i < oldCapacity ; i++) { HashEntry<K,V> e = oldTable[i]; if (e != null ) { HashEntry<K,V> next = e.next; int idx = e.hash & sizeMask; if (next == null ) newTable[idx] = e; else { HashEntry<K,V> lastRun = e; int lastIdx = idx; for (HashEntry<K,V> last = next; last != null ; last = last.next) { int k = last.hash & sizeMask; if (k != lastIdx) { lastIdx = k; lastRun = last; } } newTable[lastIdx] = lastRun; for (HashEntry<K,V> p = e; p != lastRun; p = p.next) { V v = p.value; int h = p.hash; int k = h & sizeMask; HashEntry<K,V> n = newTable[k]; newTable[k] = new HashEntry <K,V>(h, p.key, v, n); } } } } int nodeIndex = node.hash & sizeMask; node.setNext(newTable[nodeIndex]); newTable[nodeIndex] = node; table = newTable; }
扩容过程中的整体逻辑还是好理解的,不过中的两次循环还是耐人寻味的
如果抛开第一次循环,仅靠第二次循环,整体的逻辑也是能走通的
这里第一次循环用来确定链表中的一段连续部分,这些节点在扩容后依然会落到新表的同一个索引位置上。这部分链表可以直接搬迁,不需要对每个节点重新构造,这样做可以减少对象的创建和复制,提升性能
虽然有可能 lastRun 会是最后一个元素,这样第一次循环会显得多余,不过大神 Doug Lea 也说到,根据统计,如果使用默认的阈值,大概只有 1/6 的节点需要克隆
这里需要稍微注意下,扩容的大小始终是 2 的幂次(oldCapacity << 1)这样可以通过位操作(&)来计算索引,比使用取模操作(%)更高效
而 threshold 是扩容阈值,用来决定何时出发扩容,它等于 capacity * loadFactor,确保当数组填充到一定程度时开始扩容,避免哈希冲突导致性能下降
GET 相较于 put 来说,get 就很简单了
计算 hash 值,找到对应的 segment 数组中的具体位置
再找出 segment 中 HashEntry 数组的具体位置
然后就是顺着链表查找即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public V get (Object key) { Segment<K,V> s; HashEntry<K,V>[] tab; int h = hash(key); long u = (((h >>> segmentShift) & segmentMask) << SSHIFT) + SBASE; if ((s = (Segment<K,V>)UNSAFE.getObjectVolatile(segments, u)) != null && (tab = s.table) != null ) { for (HashEntry<K,V> e = (HashEntry<K,V>) UNSAFE.getObjectVolatile (tab, ((long )(((tab.length - 1 ) & h)) << TSHIFT) + TBASE); e != null ; e = e.next) { K k; if ((k = e.key) == key || (e.hash == h && key.equals(k))) return e.value; } } return null ; }
REMOVE 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 public V remove (Object key) { int hash = hash(key); Segment<K,V> s = segmentForHash(hash); return s == null ? null : s.remove(key, hash, null ); } final V remove (Object key, int hash, Object value) { if (!tryLock()) scanAndLock(key, hash); V oldValue = null ; try { HashEntry<K,V>[] tab = table; int index = (tab.length - 1 ) & hash; HashEntry<K,V> e = entryAt(tab, index); HashEntry<K,V> pred = null ; while (e != null ) { K k; HashEntry<K,V> next = e.next; if ((k = e.key) == key || (e.hash == hash && key.equals(k))) { V v = e.value; if (value == null || value == v || value.equals(v)) { if (pred == null ) setEntryAt(tab, index, next); else pred.setNext(next); ++modCount; --count; oldValue = v; } break ; } pred = e; e = next; } } finally { unlock(); } return oldValue; }
与 put 类似,remove 在一开始尝试非阻塞获取锁失败后,进入到一个获取锁的方法 scanAndLock
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 private void scanAndLock (Object key, int hash) { HashEntry<K,V> first = entryForHash(this , hash); HashEntry<K,V> e = first; int retries = -1 ; while (!tryLock()) { HashEntry<K,V> f; if (retries < 0 ) { if (e == null || key.equals(e.key)) retries = 0 ; else e = e.next; } else if (++retries > MAX_SCAN_RETRIES) { lock(); break ; } else if ((retries & 1 ) == 0 && (f = entryForHash(this , hash)) != first) { e = first = f; retries = -1 ; } } }
这里即使没有用到找出的目标节点(或者没找出),通过延迟锁重试,直到有更多信息表明节点可能需要操作,减少不必要的锁争用
并发问题分析 添加节点的操作 put 和删除节点的操作 remove 都是要加 segment 上的独占锁的,所以它们之间自然不会有问题,我们需要考虑的问题就是 get 的时候在同一个 segment 中发生了 put 或 remove 操作
put 操作的线程安全性
初始化 segment,通过 CAS 来初始化 Segment
get 遍历链表的过程中发生了 put,put 采用头插法,所以并不影响 get 操作
put 对 get 的可见性:不管是 put 修改 HashEntry 还是扩容,通过 volatile 和 UNSAFE 方法保证了可见性
remove 操作的线程安全性
如果 remove 的是头节点,那么需要将头节点的 next 设置为数组该位置的元素,table 虽然使用了 volatile 修饰,但是 volatile 并不能提供数组内部操作的可见性保证,所以源码中使用了 UNSAFE 来操作数组
如果 remove 的不是头节点,它会将要删除节点的后继节点接到前驱节点中,这里的并发保证就是 next 属性是 volatile 的
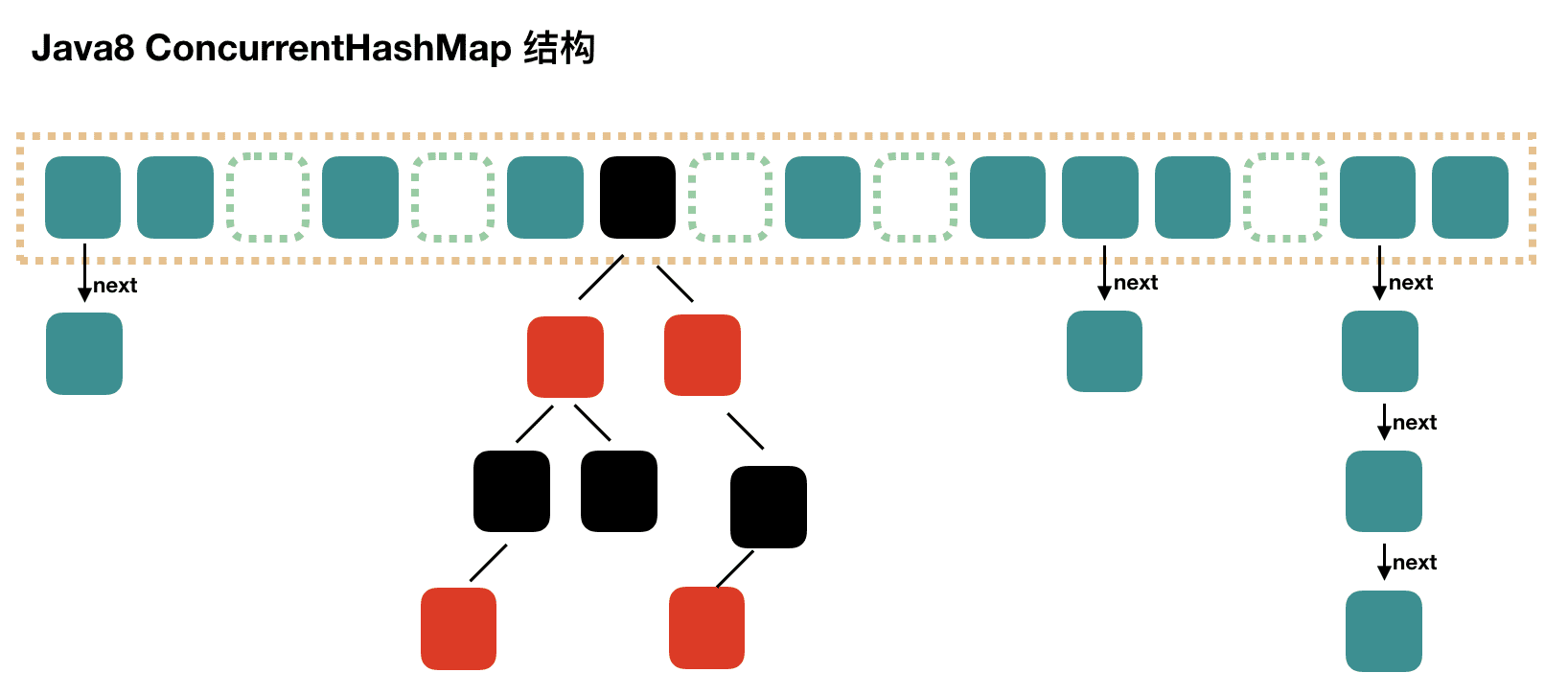
JDK 1.8 在 JDK1.8 之前,ConcurrentHashMap 是通过分段锁机制来实现的,所以其最大并发度受 Segment 的个数限制。因此,在 JDK1.8 中,ConcurrentHashMap 的实现原理摒弃了这种设计,而是选择了与 HashMap 类似的数组 + 链表 + 红黑树的方式实现,而加锁则采用 CAS 和 synchronized 实现
数据结构 关键属性:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 private static final int MAXIMUM_CAPACITY = 1 << 30 ;private static final int DEFAULT_CAPACITY = 16 ;static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8 ;private static final int DEFAULT_CONCURRENCY_LEVEL = 16 ;private static final float LOAD_FACTOR = 0.75f ;static final int TREEIFY_THRESHOLD = 8 ;static final int UNTREEIFY_THRESHOLD = 6 ;static final int MIN_TREEIFY_CAPACITY = 64 ;private static final int MIN_TRANSFER_STRIDE = 16 ;private transient volatile int sizeCtl;private static int RESIZE_STAMP_BITS = 16 ;private static final int MAX_RESIZERS = (1 << (32 - RESIZE_STAMP_BITS)) - 1 ;private static final int RESIZE_STAMP_SHIFT = 32 - RESIZE_STAMP_BITS;
关键内部类:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 static class Node <K,V> implements Map .Entry<K,V> { ...... } static final class ForwardingNode <K,V> extends Node <K,V> { ...... } static final class ReservationNode <K,V> extends Node <K,V> { ...... } static final class TreeBin <K,V> extends Node <K,V> { ...... } static final class TreeNode <K,V> extends Node <K,V> { ...... }
初始化 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 public ConcurrentHashMap () {} public ConcurrentHashMap (int initialCapacity) { if (initialCapacity < 0 ) throw new IllegalArgumentException (); int cap = ((initialCapacity >= (MAXIMUM_CAPACITY >>> 1 )) ? MAXIMUM_CAPACITY : tableSizeFor(initialCapacity + (initialCapacity >>> 1 ) + 1 )); this .sizeCtl = cap; } public ConcurrentHashMap (Map<? extends K, ? extends V> m) { this .sizeCtl = DEFAULT_CAPACITY; putAll(m); } public ConcurrentHashMap (int initialCapacity, float loadFactor) { this (initialCapacity, loadFactor, 1 ); } public ConcurrentHashMap (int initialCapacity, float loadFactor, int concurrencyLevel) { if (!(loadFactor > 0.0f ) || initialCapacity < 0 || concurrencyLevel <= 0 ) throw new IllegalArgumentException (); if (initialCapacity < concurrencyLevel) initialCapacity = concurrencyLevel; long size = (long )(1.0 + (long )initialCapacity / loadFactor); int cap = (size >= (long )MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : tableSizeFor((int )size); this .sizeCtl = cap; }
在计算初始容量时,有一个很经典的方法 tableSizeFor
1 2 3 4 5 6 7 8 9 10 11 12 private static final int tableSizeFor (int c) { int n = c - 1 ; n |= n >>> 1 ; n |= n >>> 2 ; n |= n >>> 4 ; n |= n >>> 8 ; n |= n >>> 16 ; return (n < 0 ) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1 ; }
这里是参考的 Hacker’s Delight 中的算法,类似的还有通过位移计算最小的 2 的幂
1 2 3 4 5 6 7 8 static int ceilingPowerOf2 (int x) { x = x | (x >> 1 ); x = x | (x >> 2 ); x = x | (x >> 4 ); x = x | (x >> 8 ); x = x | (x >> 16 ); return x - (x >> 1 ); }
PUT 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 public V put (K key, V value) { return putVal(key, value, false ); } final V putVal (K key, V value, boolean onlyIfAbsent) { if (key == null || value == null ) throw new NullPointerException (); int hash = spread(key.hashCode()); int binCount = 0 ; for (Node<K,V>[] tab = table;;) { Node<K,V> f; int n, i, fh; if (tab == null || (n = tab.length) == 0 ) tab = initTable(); else if ((f = tabAt(tab, i = (n - 1 ) & hash)) == null ) { if (casTabAt(tab, i, null , new Node <K,V>(hash, key, value, null ))) break ; } else if ((fh = f.hash) == MOVED) tab = helpTransfer(tab, f); else { V oldVal = null ; synchronized (f) { if (tabAt(tab, i) == f) { if (fh >= 0 ) { binCount = 1 ; for (Node<K,V> e = f;; ++binCount) { K ek; if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { oldVal = e.val; if (!onlyIfAbsent) e.val = value; break ; } Node<K,V> pred = e; if ((e = e.next) == null ) { pred.next = new Node <K,V>(hash, key, value, null ); break ; } } } else if (f instanceof TreeBin) { Node<K,V> p; binCount = 2 ; if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key, value)) != null ) { oldVal = p.val; if (!onlyIfAbsent) p.val = value; } } } } if (binCount != 0 ) { if (binCount >= TREEIFY_THRESHOLD) treeifyBin(tab, i); if (oldVal != null ) return oldVal; break ; } } } addCount(1L , binCount); return null ; }
接下来看数组为空时的初始化方法 initTable
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 private final Node<K,V>[] initTable() { Node<K,V>[] tab; int sc; while ((tab = table) == null || tab.length == 0 ) { if ((sc = sizeCtl) < 0 ) Thread.yield (); else if (U.compareAndSwapInt(this , SIZECTL, sc, -1 )) { try { if ((tab = table) == null || tab.length == 0 ) { int n = (sc > 0 ) ? sc : DEFAULT_CAPACITY; Node<K,V>[] nt = (Node<K,V>[])new Node <?,?>[n]; table = tab = nt; sc = n - (n >>> 2 ); } } finally { sizeCtl = sc; } break ; } } return tab; }
链表转红黑树 treeifyBin
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 private final void treeifyBin (Node<K,V>[] tab, int index) { Node<K,V> b; int n, sc; if (tab != null ) { if ((n = tab.length) < MIN_TREEIFY_CAPACITY) tryPresize(n << 1 ); else if ((b = tabAt(tab, index)) != null && b.hash >= 0 ) { synchronized (b) { if (tabAt(tab, index) == b) { TreeNode<K,V> hd = null , tl = null ; for (Node<K,V> e = b; e != null ; e = e.next) { TreeNode<K,V> p = new TreeNode <K,V>(e.hash, e.key, e.val, null , null ); if ((p.prev = tl) == null ) hd = p; else tl.next = p; tl = p; } setTabAt(tab, index, new TreeBin <K,V>(hd)); } } } } }
扩容 接下来就是核心方法 扩容 tryPresize
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 private final void tryPresize (int size) { int c = (size >= (MAXIMUM_CAPACITY >>> 1 )) ? MAXIMUM_CAPACITY : tableSizeFor(size + (size >>> 1 ) + 1 ); int sc; while ((sc = sizeCtl) >= 0 ) { Node<K,V>[] tab = table; int n; if (tab == null || (n = tab.length) == 0 ) { n = (sc > c) ? sc : c; if (U.compareAndSwapInt(this , SIZECTL, sc, -1 )) { try { if (table == tab) { @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node <?,?>[n]; table = nt; sc = n - (n >>> 2 ); } } finally { sizeCtl = sc; } } } else if (c <= sc || n >= MAXIMUM_CAPACITY) break ; else if (tab == table) { int rs = resizeStamp(n); if (sc < 0 ) { Node<K,V>[] nt; if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0 ) break ; if (U.compareAndSwapInt(this , SIZECTL, sc, sc + 1 )) transfer(tab, nt); } else if (U.compareAndSwapInt(this , SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2 )) transfer(tab, null ); } } }
终于到了真正的 Boss,数据迁移方法 transfer
此方法支持多线程执行,外围调用此方法的时候,会保证第一个发起数据迁移的线程,nextTab 参数为 null,之后再调用此方法的时候,nextTab 不会为 null。
阅读源码之前,先要理解并发操作的机制。原数组长度为 n,所以我们有 n 个迁移任务,让每个线程每次负责一个小任务是最简单的,每做完一个任务再检测是否有其他没做完的任务,帮助迁移就可以了,而 Doug Lea 使用了一个 stride,简单理解就是步长,每个线程每次负责迁移其中的一部分,如每次迁移 16 个小任务。所以,我们就需要一个全局的调度者来安排哪个线程执行哪几个任务,这个就是属性 transferIndex 的作用。
第一个发起数据迁移的线程会将 transferIndex 指向原数组最后的位置,然后从后往前的 stride 个任务属于第一个线程,然后将 transferIndex 指向新的位置,再往前的 stride 个任务属于第二个线程,依此类推。当然,这里说的第二个线程不是真的一定指代了第二个线程,也可以是同一个线程,这个读者应该能理解吧。其实就是将一个大的迁移任务分为了一个个任务包
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 private final void transfer (Node<K,V>[] tab, Node<K,V>[] nextTab) { int n = tab.length, stride; if ((stride = (NCPU > 1 ) ? (n >>> 3 ) / NCPU : n) < MIN_TRANSFER_STRIDE) stride = MIN_TRANSFER_STRIDE; if (nextTab == null ) { try { Node<K,V>[] nt = (Node<K,V>[])new Node <?,?>[n << 1 ]; nextTab = nt; } catch (Throwable ex) { sizeCtl = Integer.MAX_VALUE; return ; } nextTable = nextTab; transferIndex = n; } int nextn = nextTab.length; ForwardingNode<K,V> fwd = new ForwardingNode <K,V>(nextTab); boolean advance = true ; boolean finishing = false ; for (int i = 0 , bound = 0 ;;) { Node<K,V> f; int fh; while (advance) { int nextIndex, nextBound; if (--i >= bound || finishing) advance = false ; else if ((nextIndex = transferIndex) <= 0 ) { i = -1 ; advance = false ; } else if (U.compareAndSwapInt (this , TRANSFERINDEX, nextIndex, nextBound = (nextIndex > stride ? nextIndex - stride : 0 ))) { bound = nextBound; i = nextIndex - 1 ; advance = false ; } } if (i < 0 || i >= n || i + n >= nextn) { int sc; if (finishing) { nextTable = null ; table = nextTab; sizeCtl = (n << 1 ) - (n >>> 1 ); return ; } if (U.compareAndSwapInt(this , SIZECTL, sc = sizeCtl, sc - 1 )) { if ((sc - 2 ) != resizeStamp(n) << RESIZE_STAMP_SHIFT) return ; finishing = advance = true ; i = n; } } else if ((f = tabAt(tab, i)) == null ) advance = casTabAt(tab, i, null , fwd); else if ((fh = f.hash) == MOVED) advance = true ; else { synchronized (f) { if (tabAt(tab, i) == f) { Node<K,V> ln, hn; if (fh >= 0 ) { int runBit = fh & n; Node<K,V> lastRun = f; for (Node<K,V> p = f.next; p != null ; p = p.next) { int b = p.hash & n; if (b != runBit) { runBit = b; lastRun = p; } } if (runBit == 0 ) { ln = lastRun; hn = null ; } else { hn = lastRun; ln = null ; } for (Node<K,V> p = f; p != lastRun; p = p.next) { int ph = p.hash; K pk = p.key; V pv = p.val; if ((ph & n) == 0 ) ln = new Node <K,V>(ph, pk, pv, ln); else hn = new Node <K,V>(ph, pk, pv, hn); } setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true ; } else if (f instanceof TreeBin) { TreeBin<K,V> t = (TreeBin<K,V>)f; TreeNode<K,V> lo = null , loTail = null ; TreeNode<K,V> hi = null , hiTail = null ; int lc = 0 , hc = 0 ; for (Node<K,V> e = t.first; e != null ; e = e.next) { int h = e.hash; TreeNode<K,V> p = new TreeNode <K,V> (h, e.key, e.val, null , null ); if ((h & n) == 0 ) { if ((p.prev = loTail) == null ) lo = p; else loTail.next = p; loTail = p; ++lc; } else { if ((p.prev = hiTail) == null ) hi = p; else hiTail.next = p; hiTail = p; ++hc; } } ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0 ) ? new TreeBin <K,V>(lo) : t; hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0 ) ? new TreeBin <K,V>(hi) : t; setTabAt(nextTab, i, ln); setTabAt(nextTab, i + n, hn); setTabAt(tab, i, fwd); advance = true ; } } } } } }
还有一个类似的方法 helpTransfer 前面在 put 中见过
当 put 时,发现正在 transfer 的话,会调用 helpTransfer
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 final Node<K,V>[] helpTransfer(Node<K,V>[] tab, Node<K,V> f) { Node<K,V>[] nextTab; int sc; if (tab != null && (f instanceof ForwardingNode) && (nextTab = ((ForwardingNode<K,V>)f).nextTable) != null ) { int rs = resizeStamp(tab.length); while (nextTab == nextTable && table == tab && (sc = sizeCtl) < 0 ) { if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || transferIndex <= 0 ) break ; if (U.compareAndSwapInt(this , SIZECTL, sc, sc + 1 )) { transfer(tab, nextTab); break ; } } return nextTab; } return table; }
到此,整个 put 方法算是解读完了,其中的细节还需多多揣摩
GET 相较于 put 方法,get 方法要简单许多
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public V get (Object key) { Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek; int h = spread(key.hashCode()); if ((tab = table) != null && (n = tab.length) > 0 && (e = tabAt(tab, (n - 1 ) & h)) != null ) { if ((eh = e.hash) == h) { if ((ek = e.key) == key || (ek != null && key.equals(ek))) return e.val; } else if (eh < 0 ) return (p = e.find(h, key)) != null ? p.val : null ; while ((e = e.next) != null ) { if (e.hash == h && ((ek = e.key) == key || (ek != null && key.equals(ek)))) return e.val; } } return null ; }
REMOVE 有了前面 put 方法的基础,remove 方法可以快速过下就了解了
1 2 3 public V remove (Object key) { return replaceNode(key, null , null ); }
这里 remove 的实现是通过 replaceNode
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 final V replaceNode (Object key, V value, Object cv) { int hash = spread(key.hashCode()); for (Node<K,V>[] tab = table;;) { Node<K,V> f; int n, i, fh; if (tab == null || (n = tab.length) == 0 || (f = tabAt(tab, i = (n - 1 ) & hash)) == null ) break ; else if ((fh = f.hash) == MOVED) tab = helpTransfer(tab, f); else { V oldVal = null ; boolean validated = false ; synchronized (f) { if (tabAt(tab, i) == f) { if (fh >= 0 ) { validated = true ; for (Node<K,V> e = f, pred = null ;;) { K ek; if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { V ev = e.val; if (cv == null || cv == ev || (ev != null && cv.equals(ev))) { oldVal = ev; if (value != null ) e.val = value; else if (pred != null ) pred.next = e.next; else setTabAt(tab, i, e.next); } break ; } pred = e; if ((e = e.next) == null ) break ; } } else if (f instanceof TreeBin) { validated = true ; TreeBin<K,V> t = (TreeBin<K,V>)f; TreeNode<K,V> r, p; if ((r = t.root) != null && (p = r.findTreeNode(hash, key, null )) != null ) { V pv = p.val; if (cv == null || cv == pv || (pv != null && cv.equals(pv))) { oldVal = pv; if (value != null ) p.val = value; else if (t.removeTreeNode(p)) setTabAt(tab, i, untreeify(t.first)); } } } } } if (validated) { if (oldVal != null ) { if (value == null ) addCount(-1L , -1 ); return oldVal; } break ; } } } return null ; }
总结 通过回答开头的问题,来对 ConcurrentHashMap 做一个总结
ConcurrentHashMap 在 Java7 和 Java8 中实现有什么差别?Java8 解決了 Java7 中什么问题?
Java7 采用 分段锁 机制,整个 Map 被分为 16(默认) 个 Segment,每个 Segment 都是一个小的 HashMap。每个 Segment 都有自己的锁,默认配置下,最理想的情况允许最多 16 个线程同时写入
Java8 移除了 Segment 分段锁,采用数组 + 链表/红黑树,当链表长度超过 8 时,转为红黑树,当红黑树节点少于 6 时,转为链表。通过 CAS 和 synchronized 来保证并发安全,锁的颗粒度更细,锁定单个桶,支持并发扩容,多线程可以同时协助扩容
相较于 Java7,Java8 提高了并发度,降低了锁的颗粒度,提高了检索效率,提高了扩容效率
ConcurrentHashMap 在 Java7 中 Segment 数 (concurrencyLevel) 默认值是多少? 为何一旦初始化就不可再扩容?
默认并发度为 16;之所以初始化后不再进行对 Segment 数组的扩容出于以下几点考虑:
锁的复杂性:每个 Segment 本身就是一个独立的 HashMap,扩容需要重新分配 Segment 数组,为了防止在扩容过程中发现线程安全问题,就需要引入更复杂的全局锁机制
影响性能:接上述的,引入了复杂的全局锁必定就会带来性能的损耗,这与 ConcurrentHashMap 的设计初衷所违背
Thanks