深入了解 Java 各种容器（四）
2024-09-18 02:46:04 # Technical # JavaBase #Binary-Search-Tree #AVL-Tree #Red-Black-Tree #TreeMap #TreeSet

从 二叉树 到 二叉搜索树（binary search tree） 到 平衡二叉树（AVL tree） 再到 红黑树（ Red-Black tree） 最后实现 TreeMap 和 TreeSet

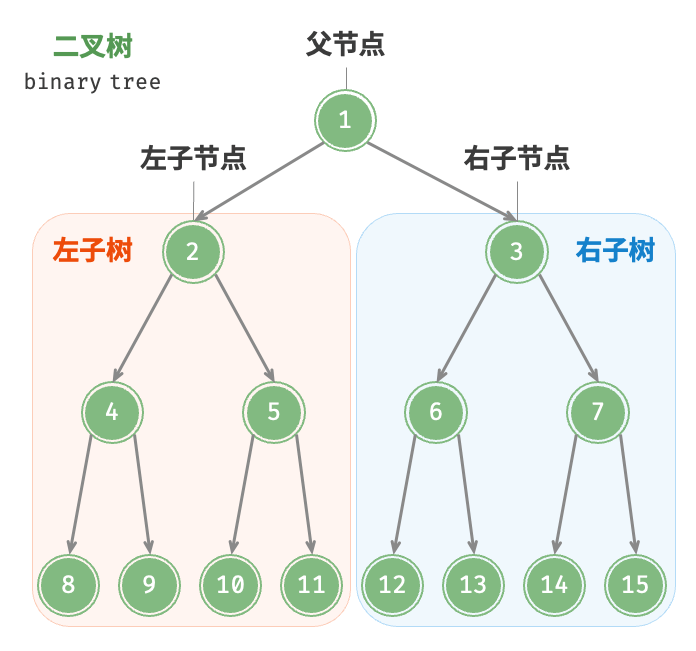
二叉树

与链表类似，二叉树的基本单元是节点，每个节点包含值、左子节点引用和右子节点引用，代表「父」与「子」之间的派生关系，体现了「一分为二」的分治逻辑

二叉树

  • 根节点：位于二叉树顶层，没有父节点（节点 1）
  • 叶节点：没有子节点的节点，其两个指针均指向 None（节点 8，9，10，11，12，13，14，15）
  • 边：连接两个节点的线段，即节点引用（指针）
  • 节点所在的层：从顶至底递增，根节点所在层为 1 （节点 4 在第 3 层）
  • 节点所在的度：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2（2）
  • 二叉树的高度：从根节点到最远叶节点所经过的边的数量（高度为 3）
  • 节点的深度：从根节点到该节点所经过的边的数量（节点 4 的深度为 2）
  • 节点的高度：从距离该节点最远的叶节点到该节点所经过的边的数量（节点 4 的高度为 1）

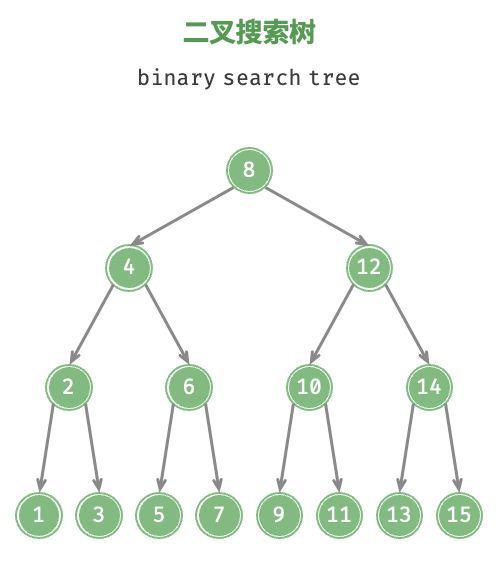
二叉搜索树

当一个二叉树满足以下条件，便可称为二叉搜索树：

  1. 左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值
  2. 左右子树也满足条件 1

二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
public class BinarySearchTree<T extends Comparable<T>> {

    private Node<T> root;

    public BinarySearchTree() {
        root = null;
    }

    public void put(T data) {
        root = insert(root, data);
    }

    private Node<T> insert(Node<T> root, T data) {
        if (root == null) {
            return new Node<>(data);
        }
        if (data.compareTo(root.data) < 0) {
            root.left = insert(root.left, data);
        } else if (data.compareTo(root.data) > 0) {
            root.right = insert(root.right, data);
        } else {
            System.out.println("已存在");
        }
        return root;
    }

    public void delete(T data) {
        root = delete(root, data);
    }

    private Node<T> delete(Node<T> root, T data) {
        if (root == null) {
            return null;
        }
        if (data.compareTo(root.data) < 0) {
            root.left = delete(root.left, data);
        } else if (data.compareTo(root.data) > 0) {
            root.right = delete(root.right, data);
        } else {
            if (root.left == null) {
                return root.right;
            } else if (root.right == null) {
                return root.left;
            } else {
                Node<T> temp = findMin(root.right);
                root.data = temp.data;
                root.right = delete(root.right, temp.data);
            }
        }
        return root;
    }

    private Node<T> findMin(Node<T> root) {
        while (root.left != null) {
            root = root.left;
        }
        return root;
    }
    
    static class Node<T> {
        T data;

        Node<T> left;

        Node<T> right;

        public Node(T data) {
            this.data = data;
        }

        public Node(T data, Node<T> left, Node<T> right) {
            this.data = data;
            this.left = left;
            this.right = right;
        }
    }
}
  • 二叉搜索树对插入的顺序有要求
  • 二叉搜索树的查找、插入、删除的时间复杂度都是 O(logn)
  • 最为复杂的是删除操作，删除时为了保证 左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值，删除时会取删除节点的 右子树中最小叶节点，将删除节点的值替换为叶节点的值，并删除右子树中该叶节点（详见 delete 方法）

DFS 与 BFS

关于二叉搜索树的遍历，存在两种遍历方式

深度优先搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
private void printDFS(Node<T> root) {
    List<List<Node<T>>> result = new ArrayList<>();
    dfs(root, 0, result);
    for (List<Node<T>> list : result) {
        for (Node<T> node : list) {
            System.out.print(node == null ? "N " : node.data + " ");
        }
        System.out.println();
    }
}

private void dfs(Node<T> root, int level, List<List<Node<T>>> result) {
    if (level == result.size()) {
        if (root != null) {
            result.add(new ArrayList<>(List.of(root)));
        } else {
            return;
        }
    } else {
        if (root != null) {
            result.get(level).add(root);
        } else {
            result.get(level).add(null);
            return;
        }
    }
    dfs(root.left, level + 1, result);
    dfs(root.right, level + 1, result);
}

广度优先搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private void printBFS(Node<T> root) {
    LinkedList<Node<T>> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int levelSize = queue.size();
        for (int i = 0; i < levelSize; i++) {
            Node<T> node = queue.removeFirst();
            if (node != null) {
                System.out.print(node.data + " ");
            } else {
                System.out.print("N ");
                continue;
            }

            queue.add(node.left);
            queue.add(node.right);
        }
        System.out.println();
    }
}

平衡二叉树

由于二叉搜索树的结构与插入及删除有关，这样其结构就会出现不可控，可能会退化为链表，这样所有操作的时间复杂度将变为 O(n)

因此，一个能在插入和删除时自动平衡树结构的平衡二叉树应运而生

节点高度

平衡二叉树在二叉树的基础上增加了一个属性——高度

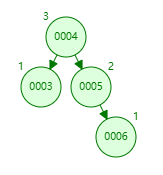
高度用来表示该节点处于平衡二叉树的层级，叶子节点的高度为 1，每距离叶子节点一个单位则高度 +1，如果左右子树的高度不一致，则取最高子树的高度

平衡二叉树

上图中，两个叶子节点 0003 和 0006 层高为 1，0005 层高为 2，根节点 0004 取较高的右子树高度 3

平衡因子

平衡因子是决定平衡二叉树是否启动自平衡的关键，通常 -1 ≤ 平衡因子 ≤ 1 时不需要调整，否则进行自平衡

某节点的平衡因子 = 该节点左子树高度 - 该节点右子树高度

如上图，

0004 节点的平衡因子 = 1 - 2 = -1

0005 节点的平衡因子 = 0 - 1 = -1

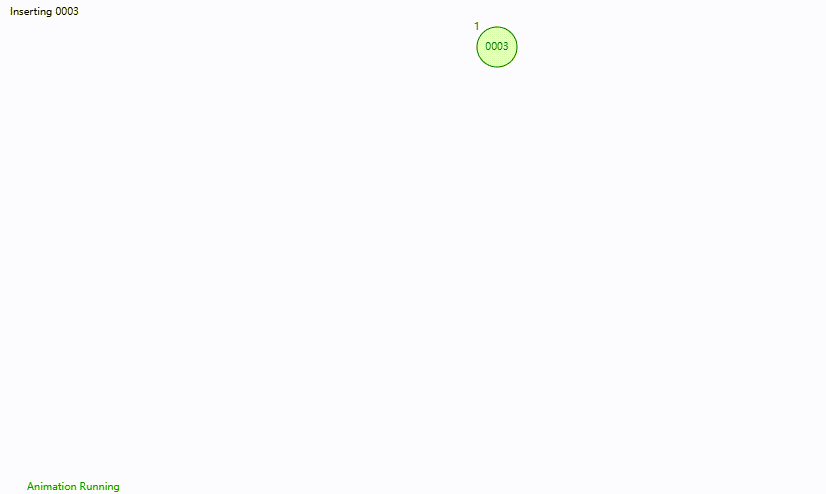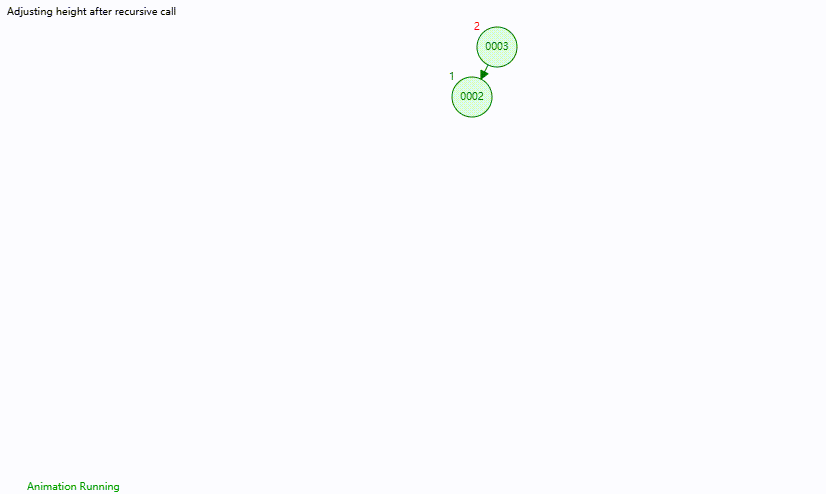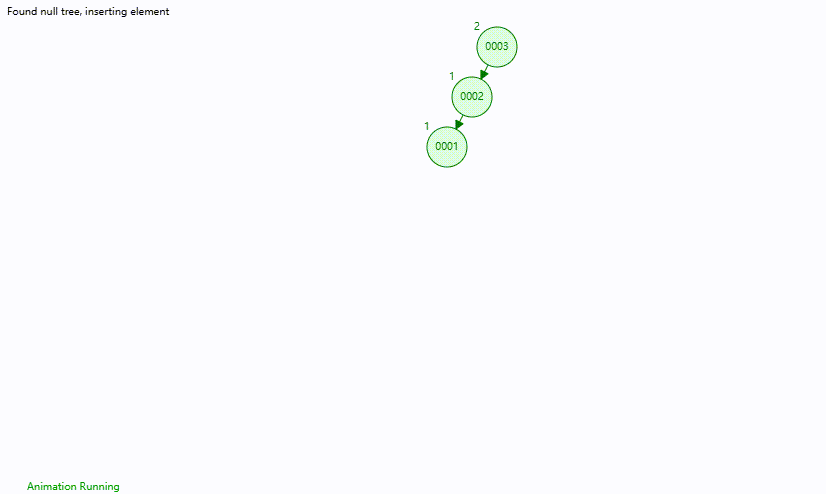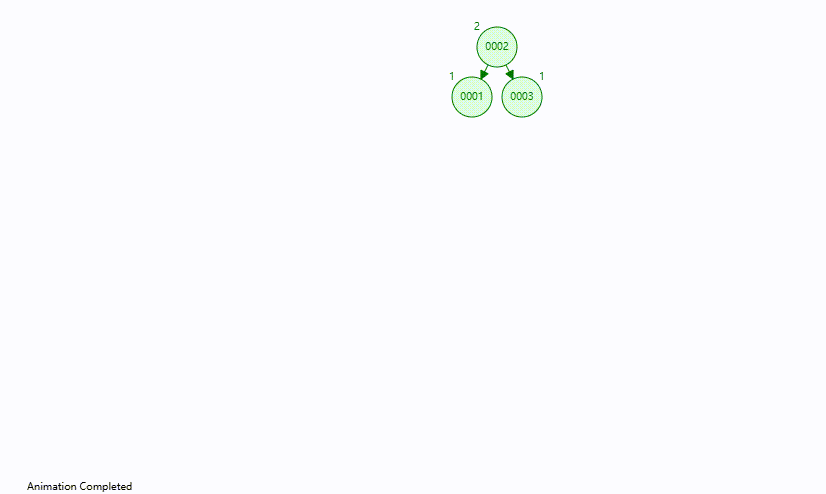
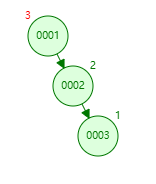
右旋

将节点 0003，0002，0001 依次插入平衡二叉树中

右旋-1

此时节点 0003 的平衡因子为 2，说明其左子树存在失衡

为保持平衡，需要将节点 0003 和 0002 进行 右旋

右旋-2

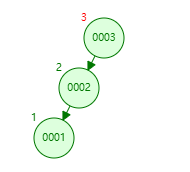
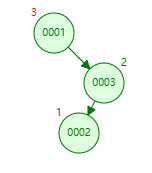
左旋

将节点 0001，0002，0003 依次插入平衡二叉树中

左旋-1

此时节点 0001 的平衡因子为 -2，说明其右子树存在失衡

为保持平衡，需要将节点 0001 和 0002 进行 左旋

左旋-2

右旋+左旋

将节点 0001，0003，0002 依次插入平衡二叉树中

右旋+左旋

此时节点 0001 的平衡因子为 -2，说明其右子树存在失衡

但 0002 < 0001 所以需要先将 0003 和 0002 进行右旋，然后再将 0001 和 0002 进行左旋

右旋+左旋

左旋 + 右旋

将节点 0003，0001，0002 依次插入平衡二叉树中

左旋+右旋

此时节点 0003 的平衡因子为 2，说明其左子树存在失衡

但 0002 > 0001 所以需要先将 0001 和 0002 进行左旋，然后再将 0003 和 0002 进行右旋

左旋+右旋

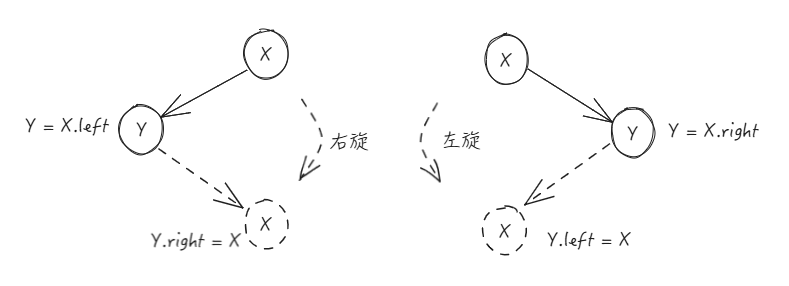
旋转的理解

右旋与左旋

  • 旋转是发生在两个节点间的操作
  • 右旋：将当前节点放到其左子节点的右子节点上
  • 左旋：将当前节点放到其右子节点的左子节点上
  • 旋转的选择：子节点 < 当前节点 => 右旋；当前节点 > 子节点 => 左旋

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
public class AVLTree<T extends Comparable<T>> {

    private Node<T> root;

    public AVLTree() {
        root = null;
    }

    public void put(T data) {
        root = insert(root, data);
    }

    private Node<T> insert(Node<T> node, T data) {
        if (node == null) {
            return new Node<>(data);
        }
        if (data.compareTo(node.data) < 0) {
            node.left = insert(node.left, data);
        } else if (data.compareTo(node.data) > 0) {
            node.right = insert(node.right, data);
        } else {
            return node;
        }

        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        int balance = getBalance(node);

        //   x
        //  y
        // z
        // 左子树过长，z < y < x
        if (balance > 1 && data.compareTo(node.left.data) < 0) {
            // 右旋
            //  y
            // z  x
            return rightRotate(node);
        }

        // x
        //  y
        //   z
        // 右子树过长，z > y > x
        if (balance < -1 && data.compareTo(node.right.data) > 0) {
            // 左旋
            //  y
            // x  z
            return leftRotate(node);
        }

        //   x
        //  y
        //   z
        // 左子树过长，z > y < x && z < x
        if (balance > 1 && data.compareTo(node.left.data) > 0) {
            // 先将左子树左旋
            //   x
            //  z
            // y
            node.left = leftRotate(node.left);
            // 再右旋
            //  z
            // y x
            return rightRotate(node);
        }

        // x
        //  y
        // z
        // 右子树过长，z < y > x && z > x
        if (balance < -1 && data.compareTo(node.right.data) < 0) {
            // 先将右子树右旋
            // x
            //  z
            //   y
            node.right = rightRotate(node.right);
            // 再左旋
            //  z
            // x y
            return leftRotate(node);
        }

        return node;
    }

    // 右旋：将当前节点旋转到其左子节点的右子节点上
    private Node<T> rightRotate(Node<T> node) {
        Node<T> l = node.left;
        Node<T> lr = l.right;

        l.right = node;
        node.left = lr;

        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        l.height = 1 + Math.max(getHeight(l.left), getHeight(l.right));

        return l;
    }

    // 左旋：将当前节点旋转到其右子节点的左子节点上
    private Node<T> leftRotate(Node<T> node) {
        Node<T> r = node.right;
        Node<T> rl = r.left;

        r.left = node;
        node.right = rl;

        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        r.height = 1 + Math.max(getHeight(r.left), getHeight(r.right));
        return r;
    }

    private int getHeight(Node<T> node) {
        if (node == null) {
            return 0;
        }
        return node.height;
    }

    private int getBalance(Node<T> node) {
        if (node == null) {
            return 0;
        }
        return getHeight(node.left) - getHeight(node.right);
    }

    public void print() {
        printBFS(root);
    }

    private void printBFS(Node<T> node) {
        if (node == null) {
            return;
        }
        Queue<Node<T>> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
            int level = queue.size();
            for (int i = 0; i < level; i++) {
                Node<T> tNode = queue.poll();
                if (tNode != null) {
                    System.out.print(tNode.data + " ");
                } else {
                    System.out.print("N ");
                    continue;
                }
                queue.add(tNode.left);
                queue.add(tNode.right);
            }
            System.out.println();
        }
    }

    private void printDFS(Node<T> node) {
        if (node == null) {
            return;
        }
        List<List<Node<T>>> result = new ArrayList<>();
        dfs(node, 0, result);
    }

    private void dfs(Node<T> node, int level, List<List<Node<T>>> result) {
        if (level == result.size()) {
            if (node != null) {
                result.add(new ArrayList<>(List.of(node)));
            } else {
                return;
            }
        } else {
            if (node != null) {
                result.get(level).add(node);
            } else {
                result.get(level).add(null);
                return;
            }
        }
        dfs(node.left, level + 1, result);
        dfs(node.right, level + 1, result);
    }

    public void delete(T data) {
        root = delete(root, data);
    }

    private Node<T> delete(Node<T> node, T data) {
        if (node == null) {
            return null;
        }
        if (data.compareTo(node.data) < 0) {
            node.left = delete(node.left, data);
        } else if (data.compareTo(node.data) > 0) {
            node.right = delete(node.right, data);
        } else {
            if (node.left == null || node.right == null) {
                node = node.left != null ? node.left : node.right;
            } else {
                Node<T> temp = minValueNode(node.right);
                node.data = temp.data;
                node.right = delete(node.right, temp.data);
            }
        }

        if (node == null) {
            return node;
        }

        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));

        int balance = getBalance(node);
        if (balance > 1 && getBalance(node.left) >= 0) {
            return rightRotate(node);
        }

        if (balance > 1 && getBalance(node.left) < 0) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }

        if (balance < -1 && getBalance(node.right) <= 0) {
            return leftRotate(node);
        }

        if (balance < -1 && getBalance(node.right) > 0) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }

        return node;
    }

    private Node<T> minValueNode(Node<T> node) {
        if (node == null) {
            return null;
        }
        if (node.left == null) {
            return node;
        }
        return minValueNode(node.left);
    }

    public static void main(String[] args) {
        AVLTree<Integer> avlTree = new AVLTree<>();
        avlTree.put(5);
        avlTree.print();
        avlTree.put(3);
        avlTree.print();
        avlTree.put(4);
        avlTree.print();
    }

    static class Node<T> {
        T data;
        Node<T> left;
        Node<T> right;
        int height;

        public Node(T data) {
            this.data = data;
            this.height = 1;
        }
    }
}

红黑树

平衡二叉树为保证树的平衡，在插入和删除的时候可能会触发 logN 次旋转，随着 N 的不断增大，旋转的次数会不断增多。那么有没有一种能减少旋转次数的结构呢？答案就是——红黑树

约束

红黑树对每个节点增加了一个节点颜色的属性

  • 每个节点的颜色要么是红色，要么是黑色

  • 根节点总是黑色

  • 叶子节点都是黑色

    这里的叶子节点实际指的是末尾的 null 节点

  • 如果一个节点是红色，那么其子节点必须是黑色

    不能存在两个相连的红色节点

  • 从任意节点到其每个叶子节点的路径上都包含相同数目的黑色节点

    黑色高度相同

旋转

红黑树的特点就是减少了旋转的次数，通过父节点与祖父节点的位置，以及父节点与叔节点的颜色来判断是否需要旋转

  • 父节点位于祖父节点的右边，且父节点是红色，叔节点是黑色，新增节点为右子节点

    红黑树-1

    上图中：祖父节点为 0001，父节点为 0002，叔节点为 NULL，新增节点为 0003

    这种情况下，只需将 0001 左旋 至 0002 的左子节点，并将 父节点置黑，祖父节点置红

    红黑树-2

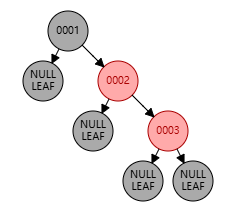
  • 父节点位于祖父节点的右边，且父节点是红色，叔节点是黑色，新增节点为左子节点

    红黑树-3

    上图中：祖父节点为 0001，父节点为 0003，叔节点为 NULL，新增节点为 0002

    这种情况下，需要先将 0003 右旋 到 0002 的右子节点，然后将 0001 左旋 到 0002 的左子节点，最后将 新增节点置黑，祖父节点置红

    红黑树-4

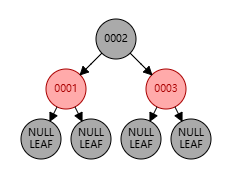
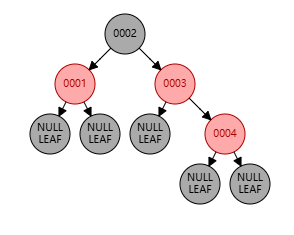
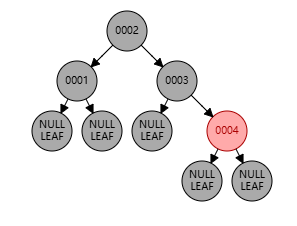
  • 父节点位于祖父节点的右边，且父节点和叔节点都是红色

    红黑树-5

    上图中：祖父节点为 0002，父节点为 0003，叔节点为 0001，新增节点为 0004

    这种情况下，无论新增节点是在左子树上还是右子树上，都 不需要旋转调整结构，只需要改变颜色，将父节点与叔节点置为黑色，祖父节点置为红色，此处祖父节点为根节点，所以还需重置为黑色

    红黑树-6

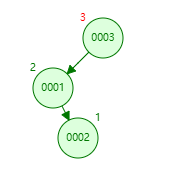
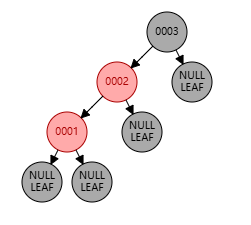
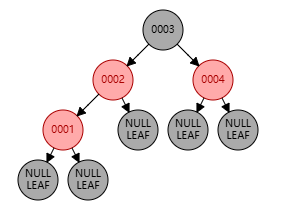
  • 父节点位于祖父节点的左边，且父节点是红色，叔节点是黑色，新增节点为左子节点

    红黑树-7

    上图中：祖父节点为 0003，父节点为 0002，叔节点为 NULL，新增节点为 0001

    这种情况下，只需将 0003 右旋 至 0002 的右子节点，并将 父节点置黑，祖父节点置红

    红黑树-8

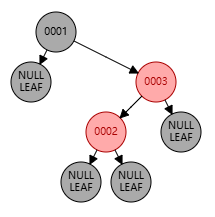
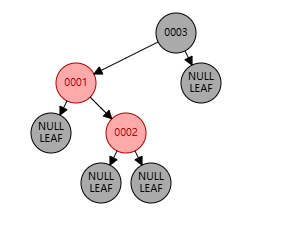
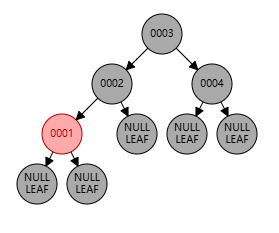
  • 父节点位于祖父节点的左边，且父节点是红色，叔节点是黑色，新增节点为右子节点

    红黑树-9

    上图中：祖父节点为 0003，父节点为 0001，叔节点为 NULL，新增节点为 0002

    这种情况下，需要先将 0001 左旋 到 0002 的左子节点，然后将 0003 右旋 到 0002 的右子节点，最后将 新增节点置黑，祖父节点置红

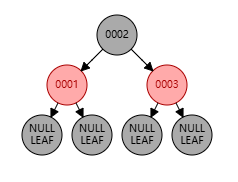
    红黑树-10

  • 父节点位于祖父节点的左边，且父节点和叔节点都是红色

    红黑树-11

    上图中：祖父节点为 0003，父节点为 0002，叔节点为 0004，新增节点为 0001

    与父节点位于祖父节点的右边，且父节点和叔节点都是红色的情况一致，都 不需要旋转调整结构，只需要改变颜色

    红黑树-12

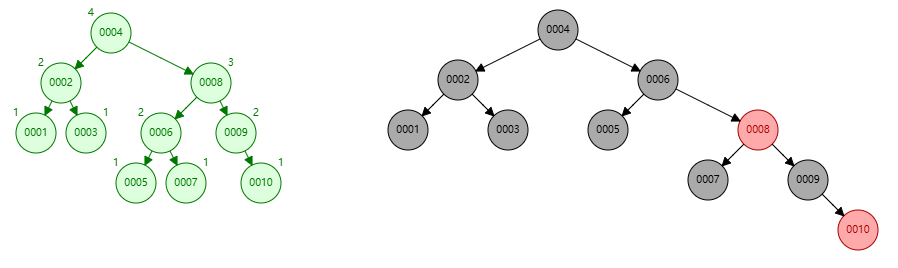
对比 AVL-Trees

将 0001~0010 分别插入平衡二叉树与红黑树中

AVL-Trees VS RedBlack-Trees

红黑树舍弃了平衡二叉树严格要求的左右子树高度差，取而代之的是节点颜色

从而牺牲部分的查找性能来换取插入和删除的性能

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
public class RBTee<T extends Comparable<T>> {

    private static final boolean RED = true;
    private static final boolean BLACK = false;

    private Node<T> root;

    public RBTee() {
        this.root = null;
    }

    public void put(T value) {
        Node<T> newNode = new Node<>(value);
        insert(newNode);
    }

    private void insert(Node<T> newNode) {
        // 找出newNode的父节点
        Node<T> current = root;
        Node<T> parent = null;
        while (current != null) {
            parent = current;
            if (newNode.data.compareTo(current.data) < 0) {
                current = current.left;
            } else {
                current = current.right;
            }
        }

        // 关联newNode与父节点
        newNode.parent = parent;
        if (parent == null) {
            root = newNode;
        } else if (newNode.data.compareTo(parent.data) < 0) {
            parent.left = newNode;
        } else {
            parent.right = newNode;
        }

        // 调整平衡
        fixAfterInsertion(newNode);
    }

    private void fixAfterInsertion(Node<T> newNode) {
        // 当newNode非root节点，且父节点为红色
        while (newNode != root && newNode.parent.color == RED) {
            Node<T> parent = newNode.parent;
            // 祖父
            Node<T> grandParent = parent.parent;
            // 判断父节点比祖父节点大还是小
            if (parent == grandParent.left) {
                // 叔节点
                Node<T> uncle = grandParent.right;
                if (uncle != null && uncle.color == RED) {
                    // Case 1：父节点与叔节点都是红色
                    parent.color = BLACK;
                    uncle.color = BLACK;
                    grandParent.color = RED;
                    newNode = grandParent;
                } else {
                    // Case 2：父节点是红色，叔节点是黑色，newNode为右子节点
                    if (newNode == parent.right) {
                        leftRotate(parent);
                        newNode = parent;
                        parent = newNode.parent;
                    }
                    // Case 3：父节点是红色，叔节点是黑色，newNode为左子节点
                    rightRotate(grandParent);
                    parent.color = BLACK;
                    grandParent.color = RED;
                    newNode = parent;
                }
            } else {
                Node<T> uncle = grandParent.left;
                if (uncle != null && uncle.color == RED) {
                    // Case 1：父节点和叔节点都是红色
                    parent.color = BLACK;
                    uncle.color = BLACK;
                    grandParent.color = RED;
                    newNode = grandParent;
                } else {
                    // Case 2：父节点是红色，叔节点是黑色，newNode为左子节点
                    if (newNode == parent.left) {
                        rightRotate(parent);
                        newNode = parent;
                        parent = newNode.parent;
                    }
                    // Case 3：父节点是红色，叔节点是黑色，newNode为右子节点
                    leftRotate(grandParent);
                    parent.color = BLACK;
                    grandParent.color = RED;
                    newNode = parent;
                }
            }
        }
        root.color = BLACK;
    }

    private void leftRotate(Node<T> node) {
        Node<T> rightSon = node.right;
        Node<T> leftGrandson = rightSon.left;

        rightSon.left = node;
        node.right = leftGrandson;
        if (leftGrandson != null) {
            // 孙节点的父节点设置为node
            rightSon.left.parent = node;
        }
        rightSon.parent = node.parent;
        if (node.parent == null) {
            root = rightSon;
        } else if (node == node.parent.left) {
            node.parent.left = rightSon;
        } else {
            node.parent.right = rightSon;
        }
        node.parent = rightSon;
    }

    private void rightRotate(Node<T> node) {
        Node<T> leftSon = node.left;
        Node<T> rightGrandson = leftSon.right;

        leftSon.right = node;
        node.left = rightGrandson;
        if (rightGrandson != null) {
            leftSon.right.parent = node;
        }
        leftSon.parent = node.parent;
        if (node.parent == null) {
            root = leftSon;
        } else if (node == node.parent.right) {
            node.parent.right = leftSon;
        } else {
            node.parent.left = leftSon;
        }
        node.parent = leftSon;
    }

    public void delete(T value) {
        Node<T> node = find(value);
        if (node == null) {
            return;
        }
        delete(node);
    }

    private void delete(Node<T> node) {
        Node<T> son, parent;
        boolean color;

        if (node.left != null && node.right != null) {
            // 替换节点为右子树的最小节点
            node = minValueNode(node.right);
        }

        if (node.left != null) {
            son = node.left;
        } else {
            son = node.right;
        }

        parent = node.parent;
        color = node.color;

        if (son != null) {
            son.parent = parent;
        }

        if (parent == null) {
            root = son;
        } else if (node == parent.left) {
            parent.left = son;
        } else {
            parent.right = son;
        }

        // 只有被删除节点为黑色，才需要调整平衡
        if (color == BLACK) {
            fixAfterDeletion(son, parent);
        }
    }

    private void fixAfterDeletion(Node<T> node, Node<T> parent) {
        // 临时节点
        Node<T> temp;

        // 当node非root节点，且node为黑色
        while (node != root && (node == null || node.color == BLACK)) {
            // 判断node在左子树还是右子树
            if (parent.left == node) {
                // node在左子树，将临时节点设置为node的兄弟节点，右子树节点
                temp = parent.right;
                // 如果node的兄弟节点的颜色为红色，为保持黑色节点数量的平衡，将node的兄弟节点的颜色设置为红色
                if (temp.color == RED) {
                    temp.color = BLACK;
                    parent.color = RED;
                    leftRotate(parent);
                    temp = parent.right;
                }

                if ((temp.left == null || temp.left.color == BLACK) &&
                        (temp.right == null || temp.right.color == BLACK)) {
                    temp.color = RED;
                    node = parent;
                    parent = node.parent;
                } else {
                    if (temp.right == null || temp.right.color == BLACK) {
                        temp.left.color = BLACK;
                        temp.color = RED;
                        rightRotate(temp);
                        temp = parent.right;
                    }
                    temp.color = parent.color;
                    parent.color = BLACK;
                    temp.right.color = BLACK;
                    leftRotate(parent);
                    node = root;
                }
            } else {
                temp = parent.left;
            }
        }
    }

    private Node<T> minValueNode(Node<T> node) {
        if (node.left == null) {
            return node;
        }
        return minValueNode(node.left);
    }

    private Node<T> find(T data) {
        Node<T> current = root;
        while (current != null) {
            if (data.compareTo(current.data) == 0) {
                return current;
            } else if (data.compareTo(current.data) < 0) {
                current = current.left;
            } else {
                current = current.right;
            }
        }
        return null;
    }

    static class Node<T> {
        T data;
        boolean color;
        Node<T> left;
        Node<T> right;
        Node<T> parent;

        public Node(T data) {
            this.data = data;
            this.color = RED;
            this.left = null;
            this.right = null;
            this.parent = null;
        }
    }
}

TreeMap

与 HashMap 和 LinkedHashMap 相似的是，他们内部都会有一个实现了 Map.Entry 的 Entry，这个 Entry 是他们存储的基本单元

TreeMap 的特点是它底层基于红黑树来实现，所以可以做到 Entry 的有序性

put

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public V put(K key, V value) {
    Entry<K,V> t = root;
    if (t == null) {
        compare(key, key); // type (and possibly null) check

        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;
    // split comparator and comparable paths
    Comparator<? super K> cpr = comparator;
    // 用默认的 Compareator 或者指定的
    if (cpr != null) {
        // 循环找到当前合适的叶子节点作为 key 的父节点（新插入的节点一定是叶子节点）
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    else {
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
        // 与上面相同，只不过这里用 key 的 compareTo 方法进行比较
        // 这里也说明，如果不指定 Comparator，那么 key 必须实现 Comparable 接口
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    Entry<K,V> e = new Entry<>(key, value, parent);
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    // 重点：旋转与调整颜色
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
private void fixAfterInsertion(Entry<K,V> x) {
    x.color = RED;

    while (x != null && x != root && x.parent.color == RED) {
        // 判断父节点在左子树还是右子树
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            // 取叔节点
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            // 判断叔节点是红还是黑
            if (colorOf(y) == RED) {
                // 自己->红 父->黑 叔->黑 祖父->红
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                // 将x设置为祖父节点，继续向上调整
                x = parentOf(parentOf(x));
            } else {
                // 如果在右子树，则需要先左旋
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateLeft(x);
                }
                // 父->黑 祖父->红
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        } else {
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    root.color = BLACK;
}

private static <K,V> Entry<K,V> parentOf(Entry<K,V> p) {
    return (p == null ? null: p.parent);
}

private static <K,V> boolean colorOf(Entry<K,V> p) {
    return (p == null ? BLACK : p.color);
}

remove

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
public V remove(Object key) {
    Entry<K,V> p = getEntry(key);
    if (p == null)
        return null;

    V oldValue = p.value;
    deleteEntry(p);
    return oldValue;
}

private void deleteEntry(Entry<K,V> p) {
    modCount++;
    size--;

    // If strictly internal, copy successor's element to p and then make p
    // point to successor.
    // 判断 p 是否同时有左子树和右子树
    if (p.left != null && p.right != null) {
        // 找出 p 的替代节点 s（p 右子树中最左的节点）
        Entry<K,V> s = successor(p);
        p.key = s.key;
        p.value = s.value;
        p = s;
    } // p has 2 children

    // Start fixup at replacement node, if it exists.
    // p 的替代节点
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);

    if (replacement != null) {
        // 用 replacement 替代掉 p
        // Link replacement to parent
        replacement.parent = p.parent;
        if (p.parent == null)
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        else
            p.parent.right = replacement;

        // Null out links so they are OK to use by fixAfterDeletion.
        p.left = p.right = p.parent = null;

        // Fix replacement
        if (p.color == BLACK)
            // 调整整个树的结构
            fixAfterDeletion(replacement);
    } else if (p.parent == null) { // return if we are the only node.
        root = null;
    } else { //  No children. Use self as phantom replacement and unlink.
        if (p.color == BLACK)
            fixAfterDeletion(p);

        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

未完待续…

Prev
2024-09-18 02:46:04 # Technical # JavaBase #Binary-Search-Tree #AVL-Tree #Red-Black-Tree #TreeMap #TreeSet
Next