深入了解 Java 各种容器（一）
2024-09-18 02:46:04 # Technical # JavaBase #ArrayList #LinkedList #ArrayDeque #PriorityQueue

Java 提供了各式各样的容器来方便开发者的使用，了解它们并正确的使用，可以有效的降低编码难度以及提高程序性能

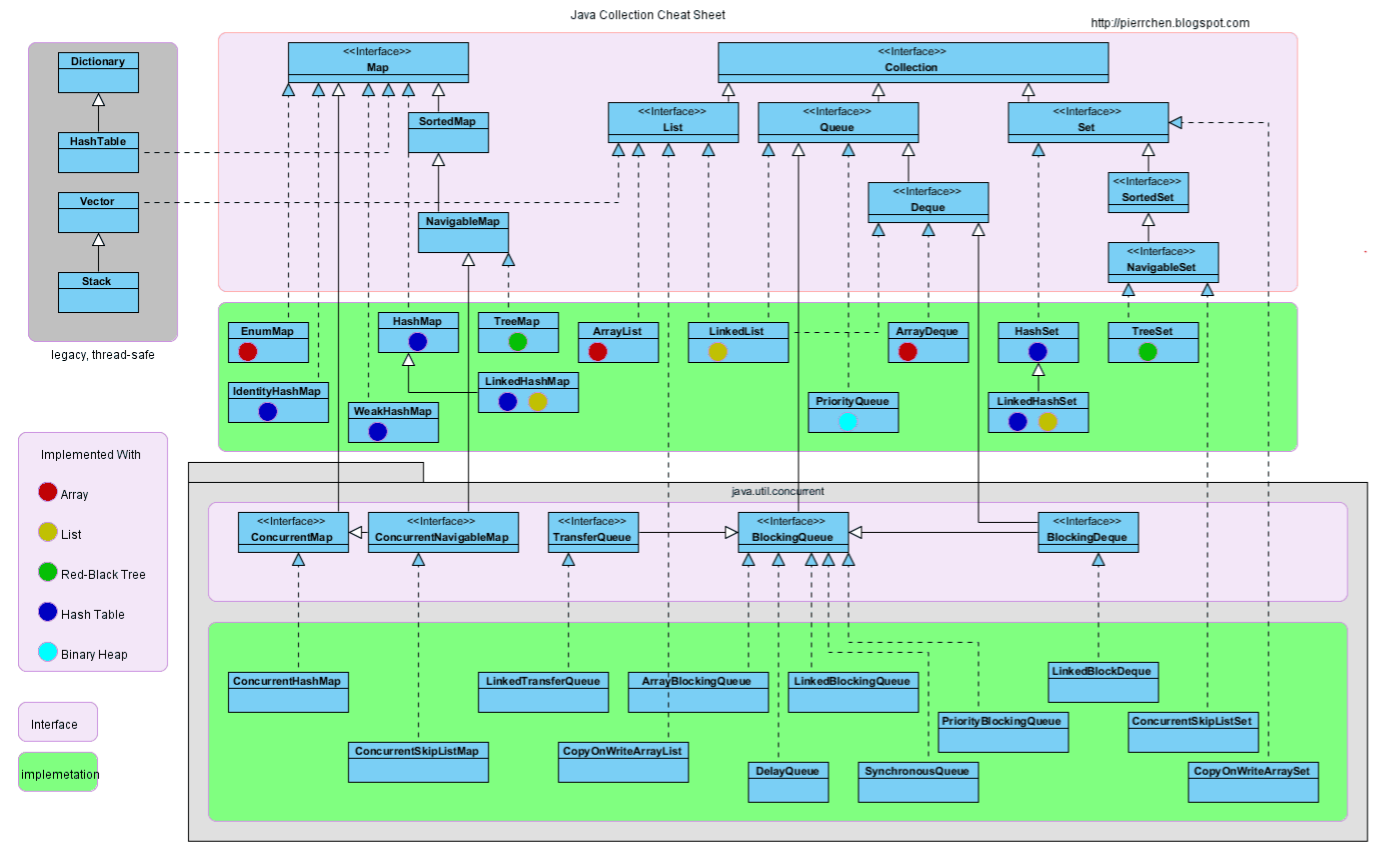
Java 容器关系

可以看出，容器大体上分为 Map 和 Collection 两种，Collection 中存储着对象的集合，Map 中存储着对象的映射

Java 容器内只能存放对象，对于基本数据类型（boolean、byte、char、short、int、long、float、double）会自动装箱/拆箱为对象类型后放入/拿出容器

ArrayList

特点

  • 有序：元素按照插入顺序排列
  • 可重复：允许存放重复元素，包括 null
  • 动态大小：可以根据实际存储的元素数量自动调整内部数组的大小
  • 随机访问：底层基于数组实现，因此可以通过索引直接访问元素，具有较快的访问速度

优点

  • 高效的随机访问：由于 ArrayList 基于数组实现，因此支持通过索引进行高效的随机访问
  • 灵活的动态大小：ArrayList 可以根据需要动态调整大小，无需手动管理数组大小
  • 易于使用：ArrayList 实现了 List 接口，提供了丰富的方法来操作元素，易于使用和理解

缺点

  • 中间元素插入和删除效率低：在 ArrayList 中间插入或删除元素时，需要将插入点之后的元素全部向后移动或将删除点之后的元素向前移动，因此效率较低
  • 连续的内存空间：ArrayList 基于数组实现，所分配的内存空间都是连续的
  • 非线程安全：没有实现同步（synchronized）

适用场景

  • 快速随机访问场景：需要频繁地通过索引进行元素访问，ArrayList 是一个很好的选择
  • 不频繁的中间插入删除：不会频繁的对中间元素进行增、删

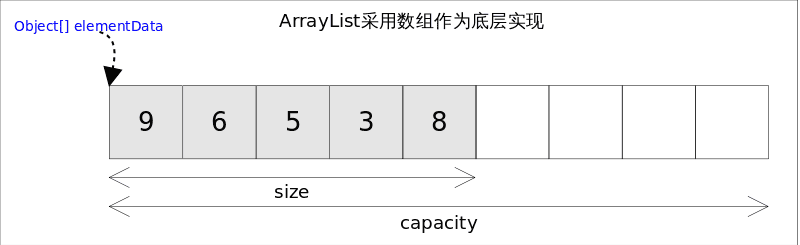
底层结构

1
2
3
4
5
6
7
8
9
/**
 * 存储 ArrayList 元素的数组缓冲区。ArrayList的容量就是该数组缓冲区的长度
 */
transient Object[] elementData; // non-private to simplify nested class access

/**
 * ArrayList 的大小（它包含的元素数量）
 */
private int size;

ArrayList 底层为数组

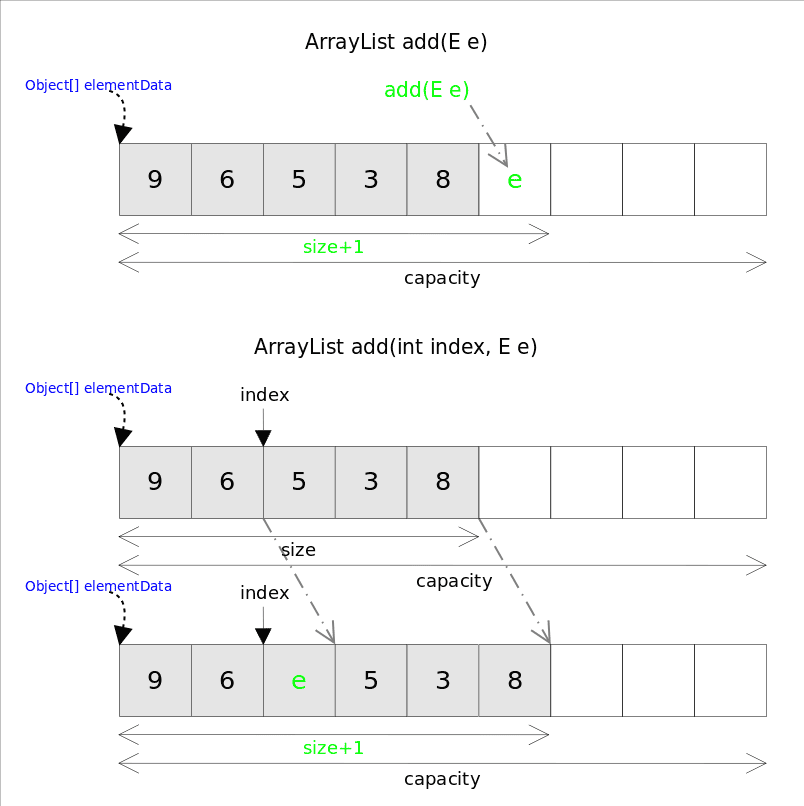
增

ArrayList 增加元素主要有两种方式，一种是 add(E e) 在数组尾端添加元素，另一种是 add(int index, E e) 在数组的指定位置添加元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public boolean add(E e) {
    // 确保容量充足（容量不足会扩容，增加 modCount）
    ensureCapacityInternal(size + 1);
    elementData[size++] = e;
    return true;
}

 public void add(int index, E element) {
     // 检查插入位置是否越界，如果 index 不在合法的范围内，会抛出 IndexOutOfBoundsException 异常
     rangeCheckForAdd(index);
     // 确保容量充足
     ensureCapacityInternal(size + 1);
     // 将原数组中指定位置后的元素往后移动一个位置，为新元素腾出插入的空间
     System.arraycopy(elementData, index, elementData, index + 1,
                      size - index);
     elementData[index] = element;
     size++;
 }

ArrayList add

除此之外，ArrayList 还提供了一次性插入多个元素的方法，addAll(Collection c) 在末尾插入多个元素，addAll(int index, Collection c) 在指定位置插入多个元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 这是 addAll 方法的第一个重载版本。它接受一个参数 c，表示要将其中的元素添加到当前列表中的另一个集合。返回一个布尔值，表示该操作是否修改了列表。如果添加了新的元素，则返回 true；否则返回 false
public boolean addAll(Collection<? extends E> c) {
    // 将集合 c 转换为数组 a
    Object[] a = c.toArray();
    // 记录要添加的新元素的数量
    int numNew = a.length;
    // 确保容量充足（容量不足会扩容，增加 modCount）
    ensureCapacityInternal(size + numNew);
    // 将数组 a 中的元素复制到列表的末尾，从索引 size 开始
    System.arraycopy(a, 0, elementData, size, numNew);
    // 更新列表的大小，增加新元素的数量
    size += numNew;
    // 返回是否成功添加了新元素的布尔值
    return numNew != 0;
}

// 这是 addAll 方法的第二个重载版本。除了接受一个集合 c 外，还接受一个索引 index，表示从指定位置开始添加新元素
public boolean addAll(int index, Collection<? extends E> c) {
    // 检查索引 index 是否越界
    rangeCheckForAdd(index);

    // 接下来的步骤与第一个重载版本类似，但在复制元素之前，需要通过 System.arraycopy 将当前位置及其后的元素向右移动，为新元素腾出空间
    Object[] a = c.toArray();
    int numNew = a.length;
    ensureCapacityInternal(size + numNew);

    int numMoved = size - index;
    if (numMoved > 0)
        System.arraycopy(elementData, index, elementData, index + numNew,
                         numMoved);

    // 将数组 a 中的元素复制到列表的指定位置 index 处，并更新列表的大小和容量
    System.arraycopy(a, 0, elementData, index, numNew);
    size += numNew;
    return numNew != 0;
}

删

删除元素也有两个版本，一个是 remove(int index) 删除指定位置的元素，另一个是 remove(Object o) 删除第一个满足 o.equals(elementData[index] 的元素。删除操作是 add 操作的逆过程，需要将删除点之后的元素向前移动一个位置。需要注意的是为了让 GC 起作用，必须显式的为最后一个位置赋值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public E remove(int index) {
    // 检查索引是否越界
    rangeCheck(index);
    // 增加 modCount，记录列表的修改次数
    modCount++;
    // 获取指定索引位置的元素
    E oldValue = elementData(index);
    // 计算需要向左移动的元素个数
    int numMoved = size - index - 1;
    if (numMoved > 0)
        // 将后面的元素向前移动一个位置
        System.arraycopy(elementData, index+1, elementData, index, numMoved);
    // 将列表中最后一个位置的元素设为 null，使其 GC
    elementData[--size] = null;
    return oldValue;
}

改

1
2
3
4
5
6
public E set(int index, E element) {
    rangeCheck(index);
    E oldValue = elementData(index);
    elementData[index] = element;
    return oldValue;
}

查

1
2
3
4
5
public E get(int index) {
    rangeCheck(index);
    // 注意类型转换
    return (E) elementData[index];
}

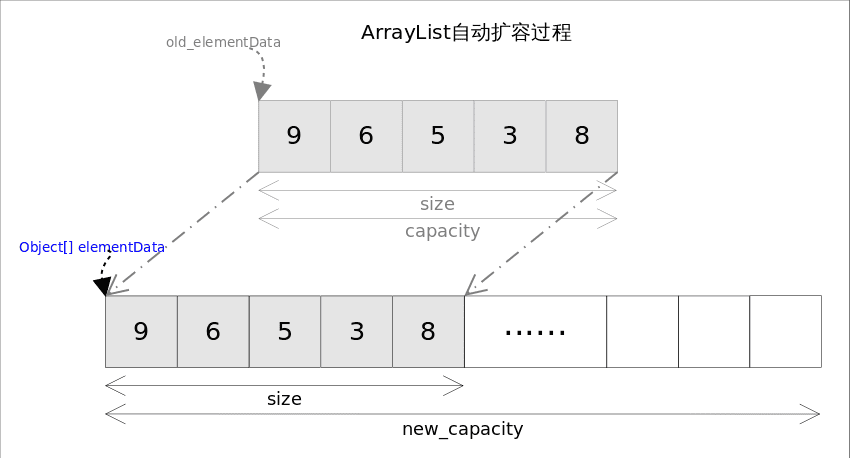
自动扩容

每向数组中添加元素时，都要去检查添加后元素的个数是否会超出当前数组的长度，如果超出，数组将会进行扩容，以满足添加数据的需求

数组扩容通过一个公开的方法 ensureCapacity(int minCapacity) 来实现

在添加大量元素前，可以调用 ensureCapacity 方法来实现手动扩容，以减少递增式再分配的数量

数组进行扩容时，会将老数组中的元素重新拷贝一份到新的数组中，每次数组容量的增长大约是其原容量的 1.5倍

这种操作的代价是很高的，因此在实际使用时，应该尽量避免数组容量的扩张。当预知要保存的元素的多少时，要在构造 ArrayList 实例时，就指定其容量，以避免数组扩容的发生

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
/**
  * 增加此ArrayList实例的容量，以确保它至少可以容纳最小容量参数指定的元素数量
  * @param minCapacity 最小容量
  */
public void ensureCapacity(int minCapacity) {
    int minExpand = (elementData != DEFAULTCAPACITY_EMPTY_ELEMENTDATA)
        // 如果是空数组，所需最小容量就为0
        ? 0
        // 默认的所需最小容量（10）
        : DEFAULT_CAPACITY;

    // 指定最小容量大于默认最小容量才进行扩容
    if (minCapacity > minExpand) {
        ensureExplicitCapacity(minCapacity);
    }
}

private static int calculateCapacity(Object[] elementData, int minCapacity) {
    if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
        return Math.max(DEFAULT_CAPACITY, minCapacity);
    }
    return minCapacity;
}

private void ensureCapacityInternal(int minCapacity) {
    ensureExplicitCapacity(calculateCapacity(elementData, minCapacity));
}

private void ensureExplicitCapacity(int minCapacity) {
    modCount++;

    // overflow-conscious code
    if (minCapacity - elementData.length > 0)
        grow(minCapacity);
}

/**
  * ArrayList 最大容量
  */
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;

/**
  * 增加容量以确保它至少可以容纳最小容量参数指定的元素数量
  * @param minCapacity 指定最小容量
  */
private void grow(int minCapacity) {
    // overflow-conscious code
    int oldCapacity = elementData.length;
    // 新容量 = 旧容量 + 旧容量 / 2
    int newCapacity = oldCapacity + (oldCapacity >> 1);
    if (newCapacity - minCapacity < 0)
        newCapacity = minCapacity;
    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);
    // 复制旧数组到新数组
    elementData = Arrays.copyOf(elementData, newCapacity);
}

private static int hugeCapacity(int minCapacity) {
    if (minCapacity < 0) // overflow
        throw new OutOfMemoryError();
    return (minCapacity > MAX_ARRAY_SIZE) ?
        Integer.MAX_VALUE :
    MAX_ARRAY_SIZE;
}

ArrayList 扩容

fail-fast

fail-fast（快速失败）机制是非线程安全集合中的一种错误机制。在用迭代器遍历一个集合对象时，如果遍历过程中对集合的结构进行了修改，则会抛出 Concurrent Modification Exception（并发修改异常）

简单来说，集合中会存在一个变量 ModCount 记录着集合的变动次数，而迭代器的内部也会存在一个变量 expectedModCount，迭代器初始化时，二者的值是相等的，迭代的过程中会反复校验它们是否相同，一旦不同则会抛出异常

1
2
3
4
final void checkForComodification() {
    if (modCount != expectedModCount)
        throw new ConcurrentModificationException();
}

会产生 ModeCount++ 的集合操作：trimToSize ensureExplicitCapacity remove fastRemove clear removeRange removeIf replaceAll sort

LinkedList

LinkedList 同时实现了 List 接口和 Deque 接口，所以它既有 List 的特点，还有 Deque 的特点

特点

  • 双向链表：基于双向链表实现的，每个元素都包含一个指向前一个元素和后一个元素的引用。这使得 LinkedList 对插入和删除操作具有较高的效率
  • 有序的：元素按插入顺序排列
  • 动态大小：可根据需要自动扩缩容
  • 允许重复：允许存储重复的元素

优点

  • 高效的插入和删除操作：由于链表结构的特性，LinkedList 在中间插入和删除元素的效率很高，不会像 ArrayList 那样需要移动大量元素
  • 不需要连续的内存空间：与数组不同，LinkedList 不需要连续的内存空间，因此在内存分配方面更加灵活
  • 适合大量的插入和删除操作：如果需要频繁地进行中间插入和删除操作，LinkedList 是一个更好的选择

缺点

  • 随机访问效率低：与 ArrayList 相比，LinkedList 不支持高效的随机访问，因为需要从头节点开始遍历到目标节点
  • 内存占用问题：每个节点需要额外的指针存储前后节点的引用，可能会导致内存占用较大
  • 随机访问效率低：需要随机访问的场景下效率较低
  • 线程不安全：未实现同步

适用场景

  • 需要频繁插入和删除操作的场景：如果应用程序需要频繁地进行插入和删除操作，特别是操作主要集中在中间位置，LinkedList 是一个很好的选择
  • 不需要频繁随机访问的场景：如果应用程序不需要频繁地通过索引进行随机访问，而是更多地进行插入、删除和遍历操作，LinkedList 是一个合适的选择
  • 强调内存利用率：由于 LinkedList 不需要预先分配空间，并且不需要连续的内存空间，因此在对内存占用有一定要求的场景下可以考虑使用 LinkedList

连续内存分配主要特点是简单高效，数据的读取和写入速度较快，但缺点是容易产生内存碎片问题，导致内存利用率降低

离散内存分配主要特点是充分利用内存空间，避免内存碎片，提高内存利用率，但缺点是分配和管理内存的算法相对复杂，会导致数据的读取和写入速度收到影响

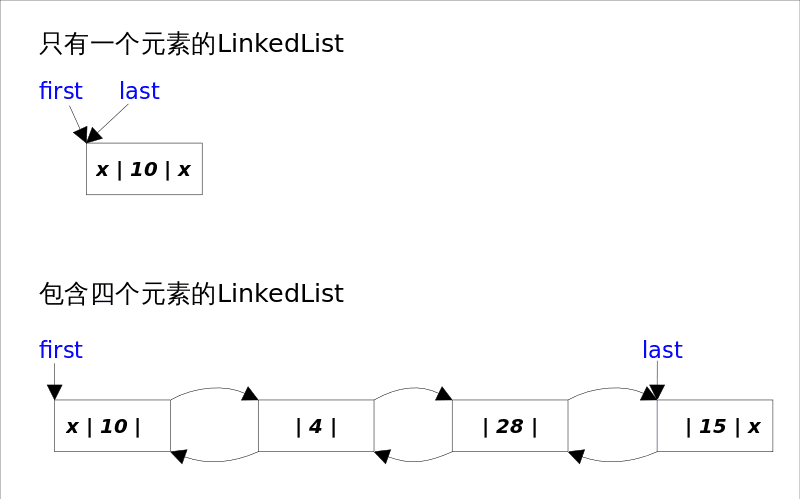
底层结构

LinkedList 底层 通过双向链表实现，双向链表的每个节点用内部类 Node 表示。LinkedList 通过 first 和 last 引用分别指向链表的第一个和最后一个元素。当链表为空的时候 first 和 last 都指向 null

1
2
3
4
5
6
7
8
9
10
11
transient int size = 0;

/**
  * 第一个元素
  */
transient Node<E> first;

/**
  * 最后一个元素
  */
transient Node<E> last;

内部类 Node

1
2
3
4
5
6
7
8
9
10
11
private static class Node<E> {
    E item;
    Node<E> next;
    Node<E> prev;

    Node(Node<E> prev, E element, Node<E> next) {
        this.item = element;
        this.next = next;
        this.prev = prev;
    }
}

LinkedList 底层结构

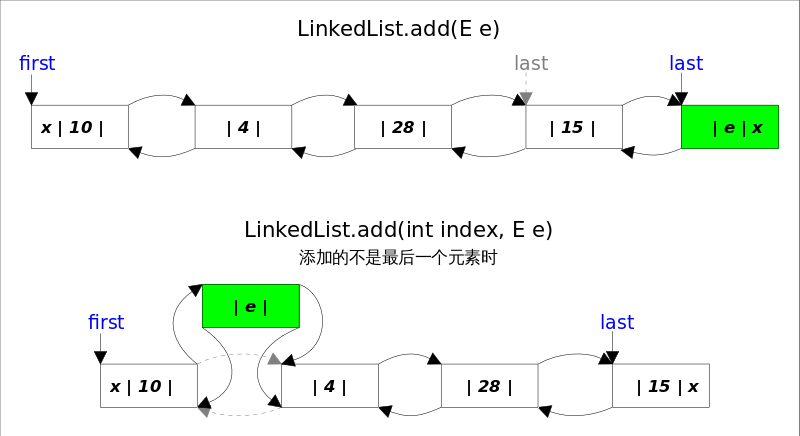
增

LinkedList 添加元素的方式主要有两种，一种是 add(E e)，该方法在 LinkedList 的末尾插入元素；另一种是 add(int index, E element)，该方法是在指定位置处插入元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
public boolean add(E e) {
    linkeLast(e);
    return true;
}

void linkLast(E e) {
    // 创建一个名为 l 的局部变量，用于保存当前列表的尾节点
    final Node<E> l = last;
    // 创建一个新的节点 newNode，并将 prev 指向当前列表的最后一个节点 l
    final Node<E> newNode = new Node<>(l, e, null);
    // 更新 last 指针，将其指向新添加的节点 newNode，表示新节点成为了列表的最后一个节点
    last = newNode;
    if (l == null)
        // 原来链表为空，这是插入的第一个元素
        first = newNode;
    else
        // 原来链表不为空，将原先的最后一个节点的 next 指向新的尾节点
        l.next = newNode;
    // 增加列表的大小
    size++;
    // 增加修改计数器
    modCount++;
}

 public void add(int index, E element) {
     // 检查插入位置是否越界
     checkPositionIndex(index);

     if (index == size)
         // 如果插入位置等于列表的大小，则调用 linkLast 方法将元素链接到列表的末尾
         linkLast(element);
     else
         // 调用 linkBefore 方法，在指定位置插入新元素
         linkBefore(element, node(index));
 }

// 获取指定索引 index 位置的节点
Node<E> node(int index) {
    // 判断索引位置是否在列表的前半部分
    if (index < (size >> 1)) {
        // 索引位置在列表的前半部分,从前往后遍历
        Node<E> x = first;
        for (int i = 0; i < index; i++)
            x = x.next;
        return x;
    } else {
        // 索引位置在列表的后半部分,从后往前
        Node<E> x = last;
        for (int i = size - 1; i > index; i--)
            x = x.prev;
        return x;
    }
}

// e（要插入的元素）和 succ（被顶到后面的节点）
 void linkBefore(E e, Node<E> succ) {
     // 创建一个名为 pred 的局部变量，用于保存指定位置之前的节点
     final Node<E> pred = succ.prev;
     // 创建一个新的节点 newNode，将新元素 e 添加到新节点中，并将其链接到 pred 和 succ 之间
     final Node<E> newNode = new Node<>(pred, e, succ);
     // 将指定位置之后的节点 succ 的 prev 指针指向新节点 newNode
     succ.prev = newNode;
     if (pred == null)
         // 原来链表为空，这是插入的第一个元素
         first = newNode;
     else
         // 将插入位置的前一个节点的 next 指向新节点
         pred.next = newNode;
     // 增加列表的大小
     size++;
     // 增加修改计数器
     modCount++;
 }

node(int index) 函数有一点小小的 trick，因为链表双向的，可以从开始往后找，也可以从结尾往前找，具体朝那个方向找取决于条件 index < (size >> 1)，也即是 index 是靠近前端还是后端

add(E e)

除此之外，LinkedList 也可以批量增加元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// 这是 addAll 方法的第一个重载版本。它接受一个参数 c，表示要将其中的元素添加到当前列表中的另一个集合。返回一个布尔值，表示该操作是否修改了列表。如果添加了新的元素，则返回 true；否则返回 false
public boolean addAll(Collection<? extends E> c) {
    // 调用了第二个重载版本的 addAll 方法，将要添加的元素从列表的末尾开始插入
    return addAll(size, c);
}

// 这是 addAll 方法的第二个重载版本。除了接受一个集合 c 外，还接受一个索引 index，表示从指定位置开始添加新元素
public boolean addAll(int index, Collection<? extends E> c) {
    // 检查索引位置是否越界
    checkPositionIndex(index);

    // 将集合 c 转换为数组 a
    Object[] a = c.toArray();
    int numNew = a.length;
    if (numNew == 0)
        // 如果要添加的新元素数量为 0，则直接返回 false
        return false;

    // 前一个节点，被顶的节点
    Node<E> pred, succ;
    if (index == size) {
        // 如果新元素加到尾端
        succ = null;
        pred = last;
    } else {
        // 新元素加到中间，找到「被顶」元素
        succ = node(index);
        pred = succ.prev;
    }

    // 遍历新元素数组
    for (Object o : a) {
        @SuppressWarnings("unchecked") E e = (E) o;
        // 新建节点，prev 指向前面的节点
        Node<E> newNode = new Node<>(pred, e, null);
        if (pred == null)
            // 原来链表为空，这是插入的第一个元素
            first = newNode;
        else
            // 将前面节点的 next 指向新节点
            pred.next = newNode;
        // 完成前节点与新节点的链接，将前节点重置为新节点，往下遍历
        pred = newNode;
    }

    if (succ == null) {
        // 「被顶」节点为 null，说明新元素加在尾部
        last = pred;
    } else {
        // 将最后一个新元素节点与「被顶」节点🔗起来
        pred.next = succ;
        succ.prev = pred;
    }

	// 增加列表的大小
    size++;
    // 增加修改计数器
    modCount++;
    return true;
}

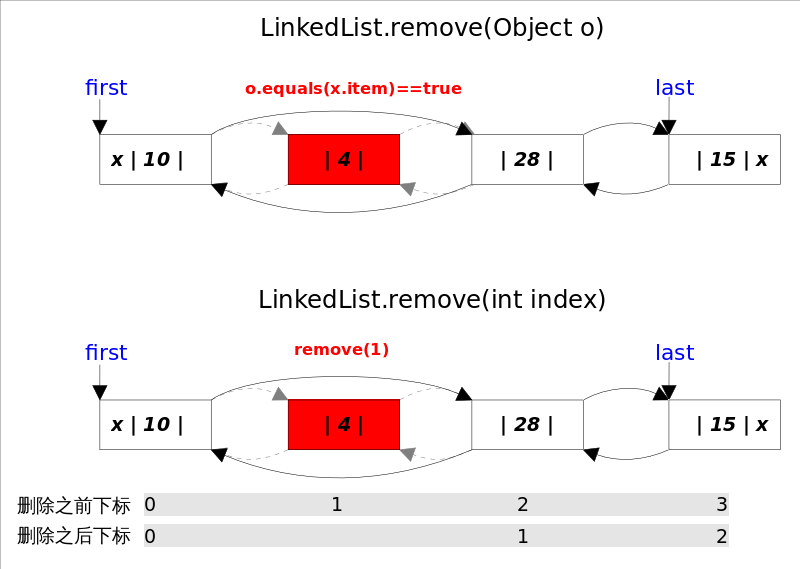
删

删除元素主要也是两种方式，一种是删除跟指定元素相等的第一个元素 remove(Object o)，另一种是删除指定下标处的元素 remove(int index)

两种方式都需要进行以下操作：

  1. 找到要删除元素的引用：在寻找被删元素引用的时候 remove(Object o) 调用的是元素的 equals 方法，而 remove(int index) 使用的是下标计数
  2. 修改相关引用：都是通过unlink(Node x)方法完成的，这里需要考虑删除元素是第一个或者最后一个时的边界情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
// 删除指定元素
public boolean remove(Object o) {
    if (o == null) {
        for (Node<E> x = first; x != null; x = x.next) {
            if (x.item == null) {
                unlink(x);
                return true;
            }
        }
    } else {
        for (Node<E> x = first; x != null; x = x.next) {
            if (o.equals(x.item)) {
                unlink(x);
                return true;
            }
        }
    }
    return false;
}

// 删除指定位置上的元素
public E remove(int index) {
    checkElementIndex(index);
    return unlink(node(index));
}

// unlink(Node<E> x)，删除一个Node
E unlink(Node<E> x) {
    final E element = x.item;
    final Node<E> next = x.next;
    final Node<E> prev = x.prev;
    // 删除的是第一个元素
    if (prev == null) {
        first = next;
    } else {
        prev.next = next;
        x.prev = null;
    }
    // 删除的是最后一个元素
    if (next == null) {
        last = prev;
    } else {
        next.prev = prev;
        x.next = null;
    }
    // let GC work
    x.item = null;
    size--;
    return element;
}

remove

除此之外，还提供了 removeFirst() 删除首节点和 removeLast() 删除尾节点的方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
// 删除首节点
public E removeFirst() {
    final Node<E> f = first;
    if (f == null)
        throw new NoSuchElementException();
    return unlinkFirst(f);
}

private E unlinkFirst(Node<E> f) {
    // assert f == first && f != null;
    final E element = f.item;
    final Node<E> next = f.next;
    f.item = null;
    f.next = null; // help GC
    first = next;
    if (next == null)
        last = null;
    else
        next.prev = null;
    size--;
    modCount++;
    return element;
}

// 删除尾节点
public E removeLast() {
    final Node<E> l = last;
    if (l == null)
        throw new NoSuchElementException();
    return unlinkLast(l);
}

private E unlinkLast(Node<E> l) {
    // assert l == last && l != null;
    final E element = l.item;
    final Node<E> prev = l.prev;
    l.item = null;
    l.prev = null; // help GC
    last = prev;
    if (prev == null)
        first = null;
    else
        prev.next = null;
    size--;
    modCount++;
    return element;
}

改

set(int index, E element) 方法将指定下标处的元素修改成指定值，也是先通过 node(int index) 找到对应下表元素的引用，然后修改 Node 中 item 的值

1
2
3
4
5
6
7
public E set(int index, E element) {
    checkElementIndex(index);
    Node<E> x = node(index);
    E oldVal = x.item;
    x.item = element;//替换新值
    return oldVal;
}

查

get(int index) 得到指定下标处元素的引用，通过调用上文中提到的 node(int index) 方法实现

1
2
3
4
5
public E get(int index) {
    // index >= 0 && index < size
    checkElementIndex(index);
    return node(index).item;
}

Queue 方法

实现了队列接口（Queue）的相关方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 查找（但不移除）队列的首节点
public E peek() {
    final Node<E> f = first;
    return (f == null) ? null : f.item;
}

// 与 peek 类似，查找（但不移除）队列的首节点，但如果队列为空，则抛出 NoSuchElementException 异常
public E element() {
    return getFirst();
}

// 查找并移除队列的首节点
public E poll() {
    final Node<E> f = first;
    return (f == null) ? null : unlinkFirst(f);
}

// 与 poll 类似，查找并移除队列的首节点，但如果队列为空，则抛出 NoSuchElementException 异常
public E remove() {
    return removeFirst();
}

// 用于将指定的元素添加到队列的尾部
public boolean offer(E e) {
    return add(e);
}

Deque 方法

实现了双端队列接口（Deque）的相关方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
// 在队列头部插入指定元素
public boolean offerFirst(E e) {
    addFirst(e);
    return true;
}

// 在队列尾部插入相关元素
public boolean offerLast(E e) {
    addLast(e);
    return true;
}

// 查找（但不移除）队列的首节点
public E peekFirst() {
    final Node<E> f = first;
    return (f == null) ? null : f.item;
}

// 查找（但不移除）队列的尾节点
public E peekLast() {
    final Node<E> l = last;
    return (l == null) ? null : l.item;
}

// 查找并移除队列的首节点
public E pollFirst() {
    final Node<E> f = first;
    return (f == null) ? null : unlinkFirst(f);
}

// 查找并移除队列的尾节点
public E pollLast() {
    final Node<E> l = last;
    return (l == null) ? null : unlinkLast(l);
}

// 将元素压入栈顶（插入队列头部）
public void push(E e) {
    addFirst(e);
}

// 将元素弹出栈顶（移除队列首节点）
public E pop() {
    return removeFirst();
}

// 移除队列中第一次出现的指定元素
public boolean removeFirstOccurrence(Object o) {
    return remove(o);
}

// 移除队列中最后一次出现的指定元素
public boolean removeLastOccurrence(Object o) {
    if (o == null) {
        for (Node<E> x = last; x != null; x = x.prev) {
            if (x.item == null) {
                unlink(x);
                return true;
            }
        }
    } else {
        for (Node<E> x = last; x != null; x = x.prev) {
            if (o.equals(x.item)) {
                unlink(x);
                return true;
            }
        }
    }
    return false;
}

ArrayDeque

Java 中有一个叫做 Stack 的类，却没有叫做 Queue 的类（Queue 是个接口）。当需要使用栈时，Java 已不推荐使用 Stack，而是推荐使用更高效的 ArrayDeque。既然 Queue 只是一个接口，当需要使用队列时也就首选 ArrayDeque 了（次选是 LinkedList）

特点

  • 双端队列：ArrayDeque 是双端队列的实现，支持在队列的两端进行元素的添加和删除操作
  • 动态大小：ArrayDeque 使用可调整大小的数组来存储元素，可以根据需要动态扩展和收缩数组的大小
  • 增删高效：ArrayDeque 在 队列的两端 进行元素的插入和删除操作的效率都很高，时间复杂度为 O(1)
  • 非 Null：不允许放入 null

优点

  • 首尾端高效的增删：对首尾端元素的插入和删除操作效率都很高
  • 动态扩容：可以根据需要动态调整大小

缺点

  • 不支持阻塞和限流：ArrayDeque 不支持容量限制和阻塞操作，因此在多线程环境下可能需要额外的同步措施来保证线程安全
  • 不适合大量的删除操作：虽然 ArrayDeque 在插入和删除操作的效率都很高，但在大量的删除操作场景下可能不如 LinkedList 高效
  • 线程不安全：与 ConcurrentLinkedDeque 不同，ArrayDeque 不是线程安全的

适用场景

  • 队列与栈的场景：需要频繁的操作首尾端节点，入列、入栈、出列、出栈
  • 单线程：没有加锁，单线程环境下性能高效
  • 不限容量：不需要对队列容量进行限制，动态调整大小

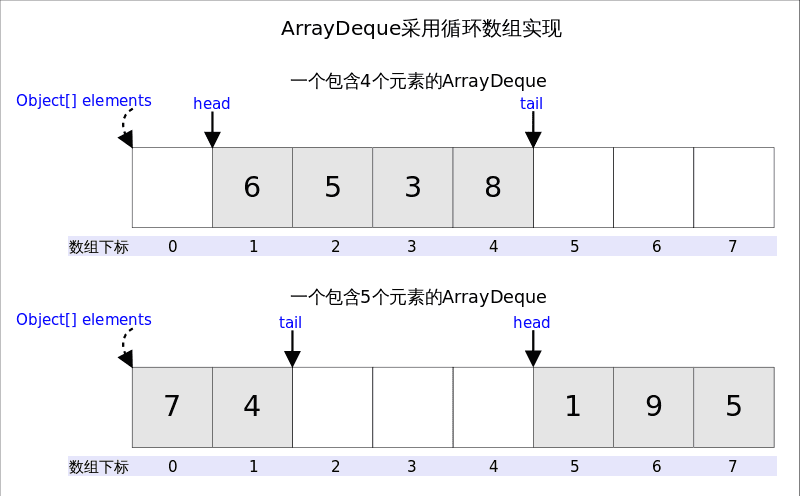
底层结构

ArrayDeque 底层通过数组实现，但为了满足可以同时在数组的两端插入或删除元素的需要，所以这个数组还是循环的，即 循环数组。数组中的任一元素都可以看作队列的起点或终点

ArrayDeque 循环数组

head 指向 首端第一个有效元素，tail 指向 尾端第一个可以插入元素的空位。因为是循环数组，所以 head 不一定总等于 0，tail 也不一定总比 head 大

0 <= head < elements.length

elements[tail] = null

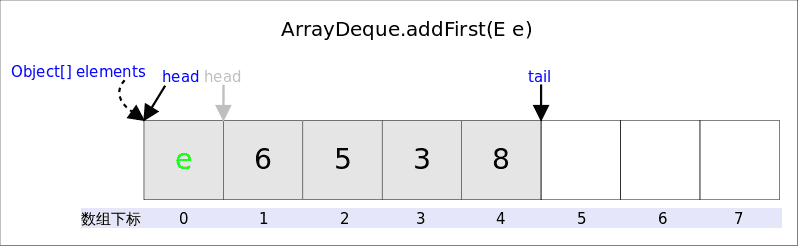
addFirst

addFirst(E e) 的作用是在 Deque 的首端插入元素，也就是在 head 的前面插入元素

1
2
3
4
5
6
7
8
9
10
public void addFirst(E e) {
    // 不允许插入 null
    if (e == null)
        throw new NullPointerException();
    // 将头指针向前移动一位，并确保它在数组的索引范围内
    elements[head = (head - 1) & (elements.length - 1)] = e;
    // 头指针等于尾指针说明数组已满，需要扩容
    if (head == tail)
        doubleCapacity();
}

addFirst(E e)

head = (head - 1) & (elements.length - 1) 这是一种非常巧妙的处理方式，head - 1 将头指针往前移一位，然后「按位与」数组的长度 -1

如果 head 大于 0，等同 rem((head - 1), (elements.length)) 相当于取余；

如果 head 等于 0，等同 elements.length - 1

不过这里有个前提，ArrayDeque 的底层数组长度为 2 的幂次方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 计算最佳容量大小
private static int calculateSize(int numElements) {
    // 默认容量 8
    int initialCapacity = MIN_INITIAL_CAPACITY;
    if (numElements >= initialCapacity) {
        initialCapacity = numElements;
        // 分别向右移动不同的位数，并使用按位或操作将结果与 initialCapacity 进行合并，以确保容量是大于等于指定元素数量的最接近的 2 的幂次方的值
        initialCapacity |= (initialCapacity >>>  1);
        initialCapacity |= (initialCapacity >>>  2);
        initialCapacity |= (initialCapacity >>>  4);
        initialCapacity |= (initialCapacity >>>  8);
        initialCapacity |= (initialCapacity >>> 16);
        initialCapacity++;

        // Too many elements, must back off
        if (initialCapacity < 0)
            // Good luck allocating 2 ^ 30 elements
            initialCapacity >>>= 1;
    }
    return initialCapacity;
}

取余「rem(x, y)」和取模「mod(x, y)」在 x 和 y 正负号一致的情况下，二者结果相同，但当 x 和 y 的符号不同时，rem 结果与 x 符号一致，mod 结果与 y 符号一致

1
2
3
4
5
6
7
8
mod(5, 2) = 1
mod(-5, 2) = 1
mod(5, -2) = -1
mod(-5, -2) = -1
rem(5, 2) = 1
rem(5, -2) = 1
rem(-5, 2) = -1
rem(-5, -2) = -1

addLast

addLast(E e) 的作用是在 ArrayDeque 的尾部插入元素，也就是在 tail 位置插入元素，tail 总是指向 下一个可插入的空位，所以只需要 elements[tail] = e 即可。插入完成后再检查空间，如果空间用完，再进行扩容即可

1
2
3
4
5
6
7
8
9
10
11
public void addLast(E e) {
    // 不允许放入null
    if (e == null)
        throw new NullPointerException();
    // 赋值
    elements[tail] = e;
    // 下标越界处理
    if ( (tail = (tail + 1) & (elements.length - 1)) == head)
        // 扩容
        doubleCapacity();
}

addLast

pollFirst

pollFirst() 的作用是删除并返回首端元素，即 head 位置处的元素。如果容器不空，直接返回 elements[head] 即可，当然还需要处理下标的问题。由于 ArrayDeque 中不允许放入 null，所以 elements[head] = null 时，意味着容器为空

1
2
3
4
5
6
7
8
9
10
11
12
public E pollFirst() {
    int h = head;
    E result = elements[head];
    // null 值意味着 deque 为空
    if (result == null)
        return null;
    // let GC work
    elements[h] = null;
    // 下标越界处理
    head = (head + 1) & (elements.length - 1);
    return result;
}

pollLast

pollLast() 的作用是删除并返回 ArrayDeque 尾端元素，即 tail 位置前面的那个元素

1
2
3
4
5
6
7
8
9
10
11
12
public E pollLast() {
    // tail 的上一个位置是最后一个元素
    int t = (tail - 1) & (elements.length - 1);
    E result = elements[t];
    // null 值意味着 deque 为空
    if (result == null)
        return null;
    // let GC work
    elements[t] = null;
    tail = t;
    return result;
}

peakFirst

peekFirst() 的作用是返回但不删除 ArrayDeque 首端元素，即 head 位置处的元素，直接返回 elements[head] 即可

1
2
3
4
public E peekFirst() {
    // elements[head] is null if deque empty
    return elements[head];
}

peakLast

peekLast() 的作用是返回但不删除 ArrayDeque 尾端元素，即 tail 位置前面的那个元素

1
2
3
public E peekLast() {
    return elements[(tail - 1) & (elements.length - 1)];
}

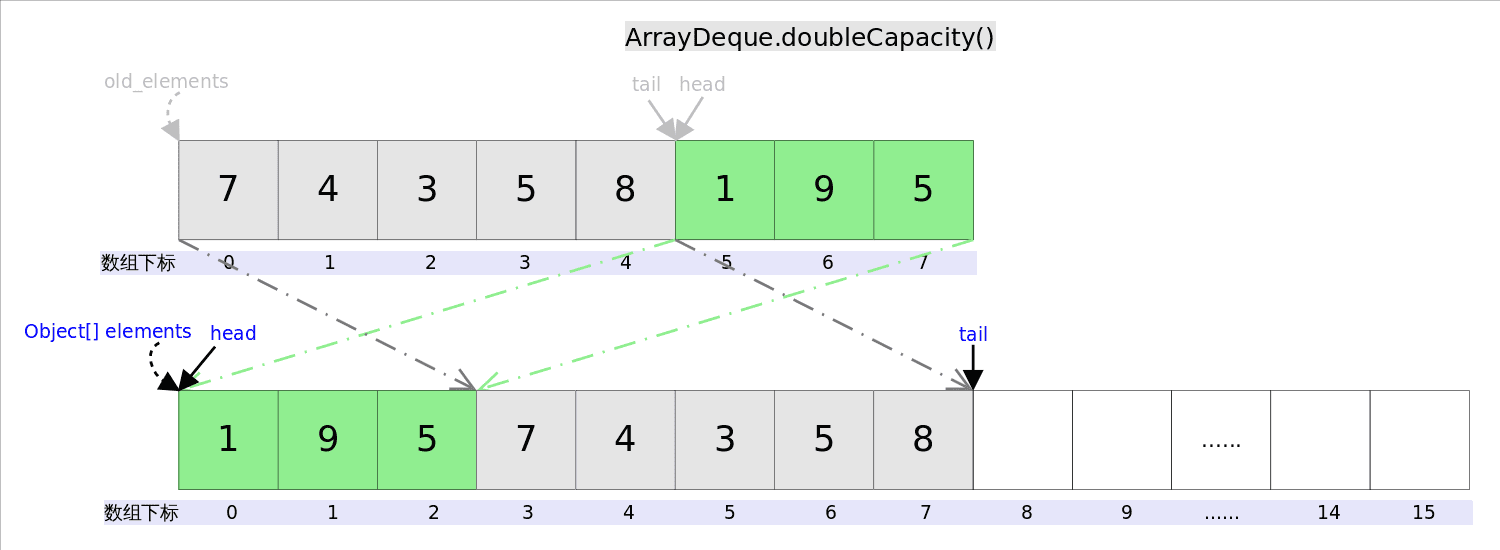
自动扩容

前面 addFirst 和 addLast 方法中涉及到了一个很重要的方法 doubleCapacity，用于自动扩容

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private void doubleCapacity() {
    assert head == tail;
    int p = head;
    int n = elements.length;
    // head 右边元素的个数
    int r = n - p;
    // 原空间的2倍
    int newCapacity = n << 1;
    if (newCapacity < 0)
        throw new IllegalStateException("Sorry, deque too big");
    Object[] a = new Object[newCapacity];
    // 复制右半部分，对应下图中绿色部分
    System.arraycopy(elements, p, a, 0, r);
    // 复制左半部分，对应下图中灰色部分
    System.arraycopy(elements, 0, a, r, p);
    elements = (E[])a;
    head = 0;
    tail = n;
}

doubleCapacity

PriorityQueue

PriorityQueue 是一个基于 Priority Heap（优先级堆）的无界优先级队列。PriorityQueue 中的元素根据自然顺序或者队列构造时提供的 Comparator 进行排序

特点

  • 优先级排序： 元素根据其优先级被排序，具有较高优先级的元素会被优先处理
  • 基于堆实现： PriorityQueue 基于 Priority Heap（优先级堆）实现，这是一种特殊的二叉堆，使得元素的插入和删除的时间复杂度为 O(log n)，其中 n 是队列的大小
  • 无界队列： PriorityQueue 在内部不会限制元素的数量，可以根据需要动态增长
  • 不允许null元素：不允许插入 null 元素，因为它会使用元素的自然顺序或者提供的比较器（Comparator）来确定元素的优先级

优点

  • 高效的插入和删除操作： PriorityQueue 基于优先级堆实现，插入和删除操作的时间复杂度为 O(log n)，其中 n 是队列中元素的数量。这使得它在需要频繁插入和删除元素的场景下表现出色
  • 自动排序： 元素在插入PriorityQueue 时会根据其优先级自动排序。这意味着高优先级的元素会在队列中更早地被处理，而低优先级的元素则会被延迟处理
  • 灵活性： PriorityQueue 可以使用元素的自然顺序或者提供的比较器（Comparator）来确定元素的优先级。这使得它适用于各种不同类型的元素和排序需求
  • 动态扩展： PriorityQueue 是一个无界队列，可以根据需要动态增长，不会受到固定容量的限制

缺点

  • 不支持随机访问： 与数组或链表不同，PriorityQueue 不支持随机访问元素。要访问具体位置的元素，只能通过迭代器或者使用 peek() 方法查看堆顶元素
  • 性能受元素比较开销影响： 如果元素的比较操作比较耗时，PriorityQueue 的性能可能会受到影响。这是因为每次插入或删除操作都需要进行元素的比较来维护堆的顺序
  • 不允许 null 元素： PriorityQueue 不允许插入 null 元素

适用场景

  • 任务调度： 当有多个任务需要按照优先级进行调度时，可以使用 PriorityQueue 来存储任务，确保高优先级的任务被优先处理
  • 事件处理： 在事件驱动的系统中，可能有多个事件需要被处理，而这些事件具有不同的优先级。PriorityQueue 可以用于按照事件优先级处理事件
  • 路由算法： 在路由算法中，需要根据不同的路由规则和条件来确定最佳路由。PriorityQueue 可以用来存储候选路由，并根据路由的优先级选择最佳路由
  • 调度器设计： 在操作系统或网络设备中，可能需要实现调度器来管理任务或消息的处理。PriorityQueue 可以用于实现调度器，确保高优先级的任务或消息能够尽快被处理
  • 资源分配： 在资源有限的环境中，需要对资源进行分配以满足不同需求。PriorityQueue 可以用于按照资源需求的优先级对资源进行分配

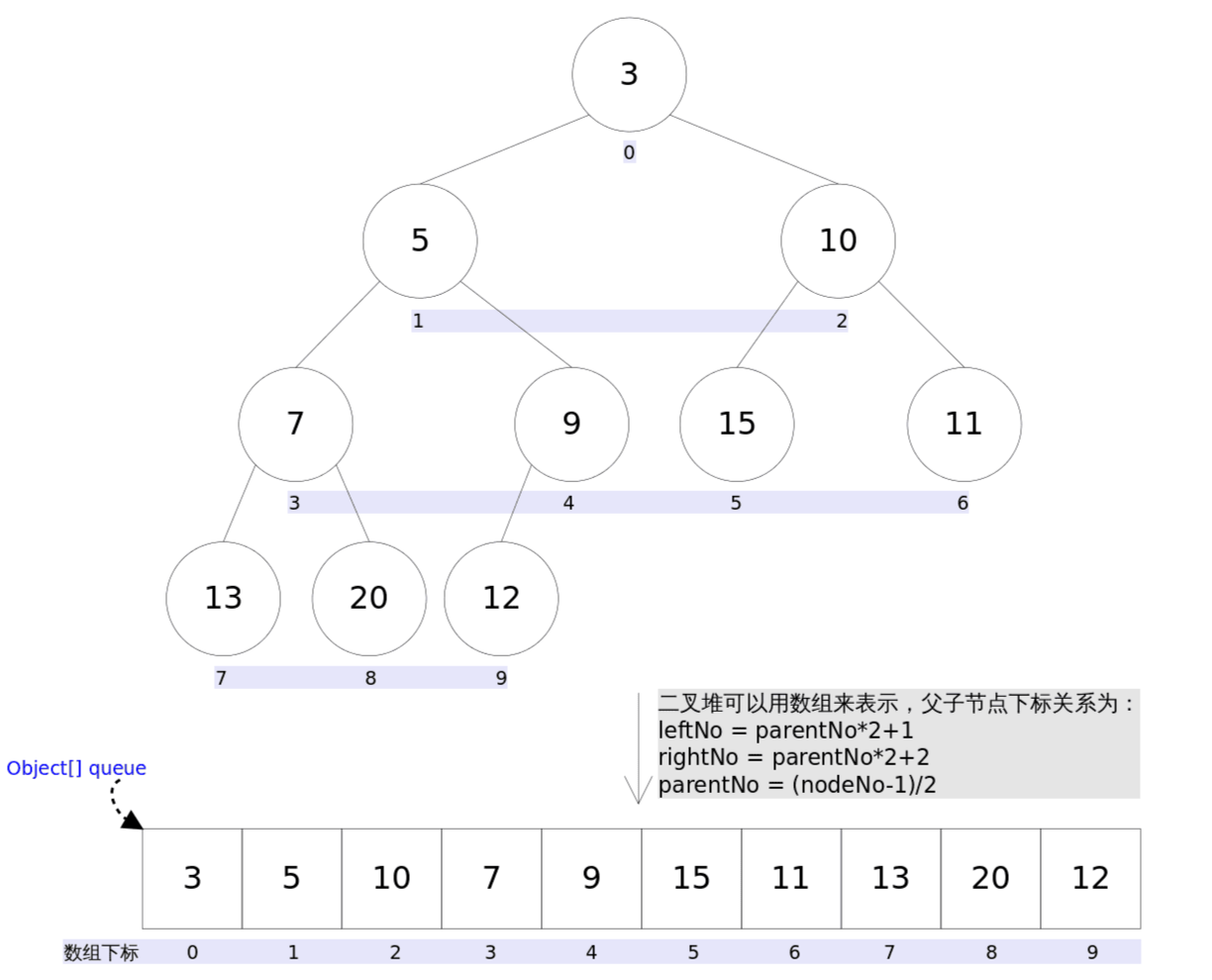
底层结构

PriorityQueue 的底层是一个通过数组实现的 Balanced Binary Heap（平衡二叉堆）

1
transient Object[] queue

queue[0] 为最低值的元素，queue[n] 的两个子级是 queue[2n + 1] 和 queue[2n + 2]

PriorityQueue 数组实现平衡二叉堆

可以看出底层数组中存放的元素并非「完全有序」的，这是 因为 PriorityQueue 只能保证「堆顶」元素为最小（小顶堆）或最大（大顶堆）

因此，PriorityQueue 的迭代器遍历出来的顺序也不会是有序的，需要通过 poll 方法依次「出堆」来保证有序

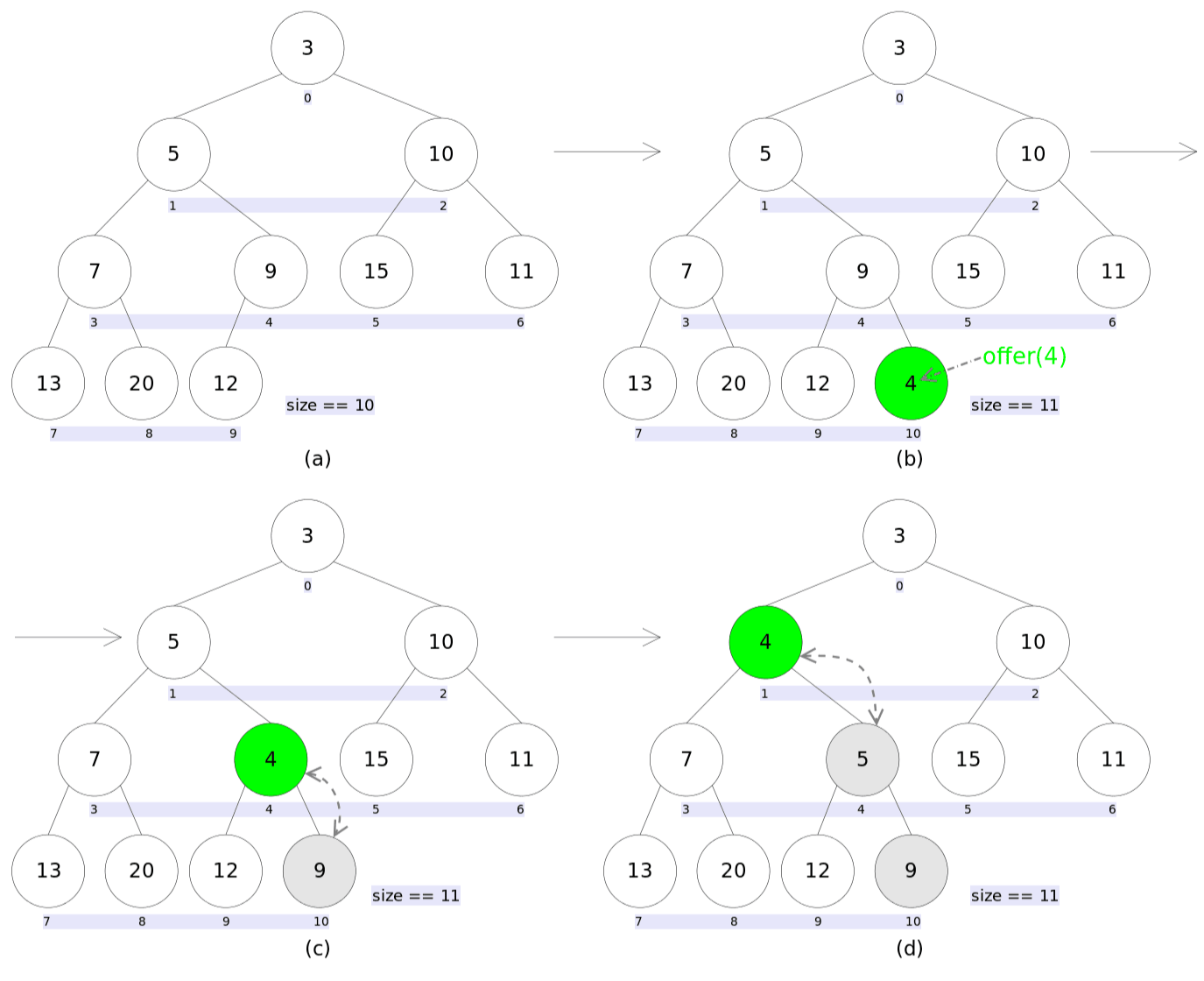
add 和 offer

add(E e) 和 offer(E e) 实现上没有任何区别，只是一个来自 Collection 一个来自 Queue

Queue 之所有在继承 Collection 的情况下，有了一个 add(E e) 后还增加一个 offer(E e)，是考虑到了容量受限的队列。对于容量受限的队列，add(E e) 超过容量限制会抛出 java.lang.IllegalStateException 异常，而 offer(E e) 不会抛出异常，而是通过返回 ture/false 来表示是否添加成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
public boolean add(E e) {
    return offer(e);
}

public boolean offer(E e) {
    // 判断新增元素是否为 null
    if (e == null)
        throw new NullPointerException();
    // 增加修改次数
    modCount++;
    int i = size;
    // 检查容量是否达到上限
    if (i >= queue.length)
        // 扩容
        grow(i + 1);
    // 关键方法：插入新元素并根据优先级调整 priority heap
    siftUp(i, e);
    // 更新元素数量
    size = i + 1;
    return true;
}

private void siftUp(int k, E x) {
    // 判断是否有通过构造函数提供比较器
    if (comparator != null)
        siftUpUsingComparator(k, x, queue, comparator);
    else
        siftUpComparable(k, x, queue);
}

// 在没提供比较器的情况下，根据元素的自然顺序进行插入和调整
private static <T> void siftUpComparable(int k, T x, Object[] es) {
    // 将要插入的 x 转为 Comparable 类型，方便后续的比较
    Comparable<? super T> key = (Comparable<? super T>) x;
    // k 为 0 时，说明到达根节点
    while (k > 0) {
        // (k-1)/2 找到父节点索引
        int parent = (k - 1) >>> 1;
        // 获取父节点
        Object e = es[parent];
        // 与父节点比较
        if (key.compareTo((T) e) >= 0)
            // 如果大于父节点，说明到达合适位置，跳出循环
            break;
        // 本次循环中的「父节点」不合适，将其下移
        es[k] = e;
        // 更新 k 为本次循环中的「父节点」索引
        k = parent;
    }
    // 找到合适位置 k，放入新元素
    es[k] = key;
}

// 用于在提供了比较器的情况下，根据比较器进行插入和调整
// 整个过程同 siftUpComparable 不同之处在于使用了自定义的比较器
private static <T> void siftUpUsingComparator(
    int k, T x, Object[] es, Comparator<? super T> cmp) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = es[parent];
        if (cmp.compare(x, (T) e) >= 0)
            break;
        es[k] = e;
        k = parent;
    }
    es[k] = x;
}

offer(E e)

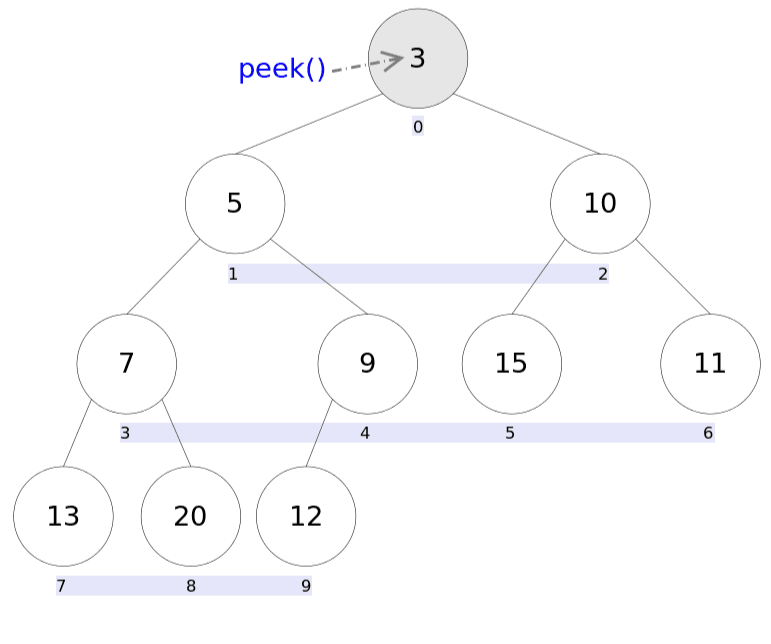
peak

返回根节点（堆顶）的元素

1
2
3
public E peek() {
    return (E) queue[0];
}

peak

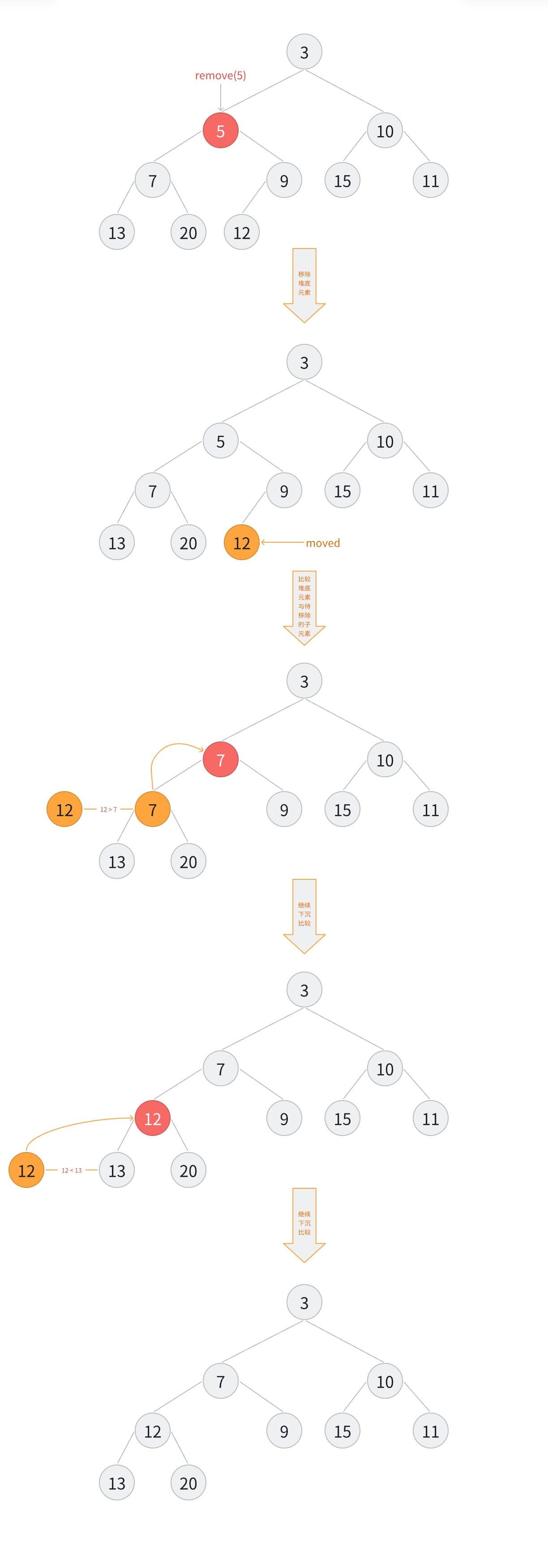
remove

remove(Object o) 删除队列中 o.equals(E) 的元素，返回 true/false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
public boolean remove(Object o) {
    // 获取待删除元素的索引
    int i = indexOf(o);
    if (i == -1)
        // 不存在直接返回 false
        return false;
    else {
        // 调用 removeAt(i) 方法进行移除
        removeAt(i);
        return true;
    }
}

// 删除队列中的第 i 个元素
E removeAt(int i) {
    // 获取队列数组
    final Object[] es = queue;
    // 增加修改计数
    modCount++;
    // 将队列大小 -1 并保存到变量 s 中
    int s = --size;
    if (s == i)
        // 如果恰好是最后一个元素，直接置 null 即可
        es[i] = null;
    else {
        // 先获取最后一个元素 moved
        E moved = (E) es[s];
        // 将最后位置置 null
        es[s] = null;
        // 将 moved 插入 i 处并向下调整
        siftDown(i, moved);
        if (es[i] == moved) {
            // 如果下沉没找到合适位置，调用 siftUp(i, moved) 进行上浮操作
            siftUp(i, moved);
            if (es[i] != moved)
                return moved;
        }
    }
    return null;
}

// 下沉：移除 k 处元素，插入 x，并向下调整整个堆的平衡
private void siftDown(int k, E x) {
    if (comparator != null)
        // 指定比较器下沉
        siftDownUsingComparator(k, x, queue, size, comparator);
    else
        // 未指定比较器下沉
        siftDownComparable(k, x, queue, size);
}

// 未指定比较器下沉：k-移除处索引 x-填充元素 es-队列数组 n-队列长度
private static <T> void siftDownComparable(int k, T x, Object[] es, int n) {
    // 将 x 转换为Comparable类型的对象 key
    Comparable<? super T> key = (Comparable<? super T>)x;
    // 计算堆的中点位置，即最后一个「非叶子节点」的索引
    int half = n >>> 1;
    // 循环 k 小于中点位置，因为只有非叶子节点才需要进行下沉
    while (k < half) {
        // 找到移除处的子节点：2k+1
        int child = (k << 1) + 1;
        // 保存子节点到变量 c
        Object c = es[child];
        // 获取右子节点索引
        int right = child + 1;
        // 比较左右两个子节点的大小
        if (right < n &&
            ((Comparable<? super T>) c).compareTo((T) es[right]) > 0)
            // 如果右子节点要小于左子节点，那么选择较小的右子节点
            c = es[child = right];
        // 比较待填充元素 key 和较小的子节点
        if (key.compareTo((T) c) <= 0)
            // 如果 key 比子节点小，说明找到了插入位置，结束循环
            break;
        // 否则，将较小子节点移动到移除处 k 的位置
        es[k] = c;
        // 将 k 置为较小子节点索引，开始下一轮循环
        k = child;
    }
    // 结束循环后，将待插入元素 x 放置到指定位置
    es[k] = key;
}

// 指定比较器下沉过程同上
private static <T> void siftDownUsingComparator(
    int k, T x, Object[] es, int n, Comparator<? super T> cmp) {
    int half = n >>> 1;
    while (k < half) {
        int child = (k << 1) + 1;
        Object c = es[child];
        int right = child + 1;
        if (right < n && cmp.compare((T) c, (T) es[right]) > 0)
            c = es[child = right];
        if (cmp.compare(x, (T) c) <= 0)
            break;
        es[k] = c;
        k = child;
    }
    es[k] = x;
}

// 上浮：移除 k 处元素，插入 x，并向上调整整个堆的平衡
private void siftUp(int k, E x) {
    if (comparator != null)
        siftUpUsingComparator(k, x, queue, comparator);
    else
        siftUpComparable(k, x, queue);
}

// 未指定比较器上浮：k-移除处索引 x-填充元素 es-队列数组 n-队列长度
private static <T> void siftUpComparable(int k, T x, Object[] es) {
    // 将 x 转换为Comparable对象 key
    Comparable<? super T> key = (Comparable<? super T>) x;
    // 根节点无法上浮，所以循环 k > 0 
    while (k > 0) {
        // 计算移除处父节点索引：(k-1)/2
        int parent = (k - 1) >>> 1;
        // 获取父节点元素并保存到变量 e
        Object e = es[parent];
        // 比较待填充元素与父节点元素
        if (key.compareTo((T) e) >= 0)
            // 如果待填充元素大于等于父节点元素，结束循环
            break;
        // 否则，将父节点放入移除处 k 的位置上
        es[k] = e;
        // k 置为父节点处，开始下一轮循环
        k = parent;
    }
    // 结束循环后，将 x 填充到合适的位置
    es[k] = key;
}

// 同未指定比较器
private static <T> void siftUpUsingComparator(
    int k, T x, Object[] es, Comparator<? super T> cmp) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = es[parent];
        if (cmp.compare(x, (T) e) >= 0)
            break;
        es[k] = e;
        k = parent;
    }
    es[k] = x;
}

remove(5)

poll

poll() 是用来获取队列的首个元素并将其删除，处理过程与 remove(Object o) 类似

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public E poll() {
    // 队列数组
    final Object[] es;
    // 队首元素
    final E result;

    // 确保队列不为空
    if ((result = (E) ((es = queue)[0])) != null) {
        // 增加修改计数
        modCount++;
        // 队尾索引
        final int n;
        // 队尾元素
        final E x = (E) es[(n = --size)];
        // 队列最后一个元素置 null
        es[n] = null;
        if (n > 0) {
            final Comparator<? super E> cmp;
            // 判断是否提供比较器
            if ((cmp = comparator) == null)
                // 使用自然比较器向下调整，移除 0 处的元素，插入 x，向下调整，过程同 remove
                siftDownComparable(0, x, es, n);
            else
                // 使用自定义比较器向下调整
                siftDownUsingComparator(0, x, es, n, cmp);
        }
    }
    return result;
}

自动扩容

PriorityQueue 在 add 和 offer 的时候，如果队列的数组容量不够，就会进行自动扩容的操作

1
2
3
4
5
6
7
// minCapacity：最小容量
private void grow(int minCapacity) {
    int oldCapacity = queue.length;
    // 计算新容量：如果容量小于 64 就 +2，否则 *2，至少 (min - old)
    int newCapacity = ArraysSupport.newLength(oldCapacity, minCapacity - oldCapacity, oldCapacity < 64 ? oldCapacity + 2 : oldCapacity >> 1);
    queue = Arrays.copyOf(queue, newCapacity);
}

Thanks

CarpenterLee/JCFInternals: 深入理解Java集合框架

Prev
2024-09-18 02:46:04 # Technical # JavaBase #ArrayList #LinkedList #ArrayDeque #PriorityQueue
Next